
接求∬2e少dc,其中D是以0,0,1,0,) 为顶点的三角形 y (0,1) (1,) 解e少无法用初等函数表示, .积分时应先对x积分, 旷rerw=rer -e=小er-3
解 2 2 y D x e dxdy 1 2 2 0 0 y y dy x e dx 2 3 1 0 3 y y e dy 2 2 1 2 0 6 y y e dy 1 2 (1 ). 6 e 2 2 (0,0),(1,1),(0,1) . y D x e dxdy D 求 ,其中 是以 为顶点的三角形 2 y e dy x 无法用初等函数表示, 积分时应先对 积分, o x y D (0,1) (1,1)

例4计算二重积分 j∬rd,其中 D D={,y0≤x≤1,0≤y≤1. 解设D={(x,y)0≤x≤1,0≤y≤, D2={(x,y0≤x≤1,x≤y≤1, ∬=∬eat+o D -∬edrd+j∬erdu 成=2ared=dred+∫dea =e-1
例4 计算二重积分 2 2 max{ , }d d , x y D e x y 其中 D x y x y {( , ) 0 1,0 1}. x y O 解 1 1 D2 D1 设 1 D x y x y x {( , ) 0 1,0 }, 2 D x y x x y {( , ) 0 1, 1}, 2 2 max{ , }d d x y D e x y 2 2 1 max{ , }d d x y D e x y 2 2 2 max{ , }d d x y D e x y 2 1 d d x D e x y 2 2 d d y D e x y 1 2 0 0 d d x x x e y 1 2 0 0 d d y y y e x e 1. 1 2 0 0 ( 2 d d ) x x x e y 或

计算积分I=∬川ly-x21do, 其中(o)为:0≤x≤1,0≤y≤1. 解 I= (o2) 0 心-xdo+∫(x2-yao 02 4,1 11 15'10 30
2 | | , ( ) : 0 1,0 1. I y x d x y 计算积分 其中 为 解 o x y 1 ( ) 1 ( ) I 2 1 2 ( )d y x 2 2 ( )d x y 10 1 15 4 . 30 11
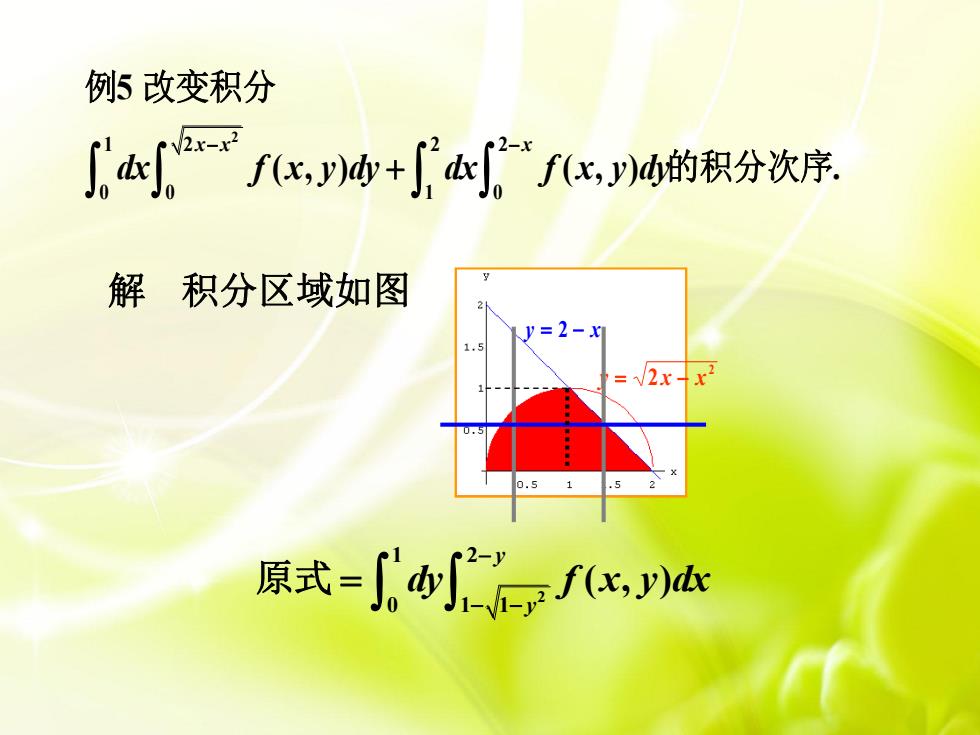
例5改变积分 d小=f+厂杰广f化o的积分次序 解积分区域如图 y=2-x 1. =√2xx 原式=
y 2 x 2 y 2 x x 解 积分区域如图 2 1 2 2 2 0 0 1 0 5 ( , ) ( , ) . x x x dx f x y dy dx f x y dy 例 改变积分 的积分次序 2 1 2 0 1 1 ( , ) y y dy f x y dx 原式
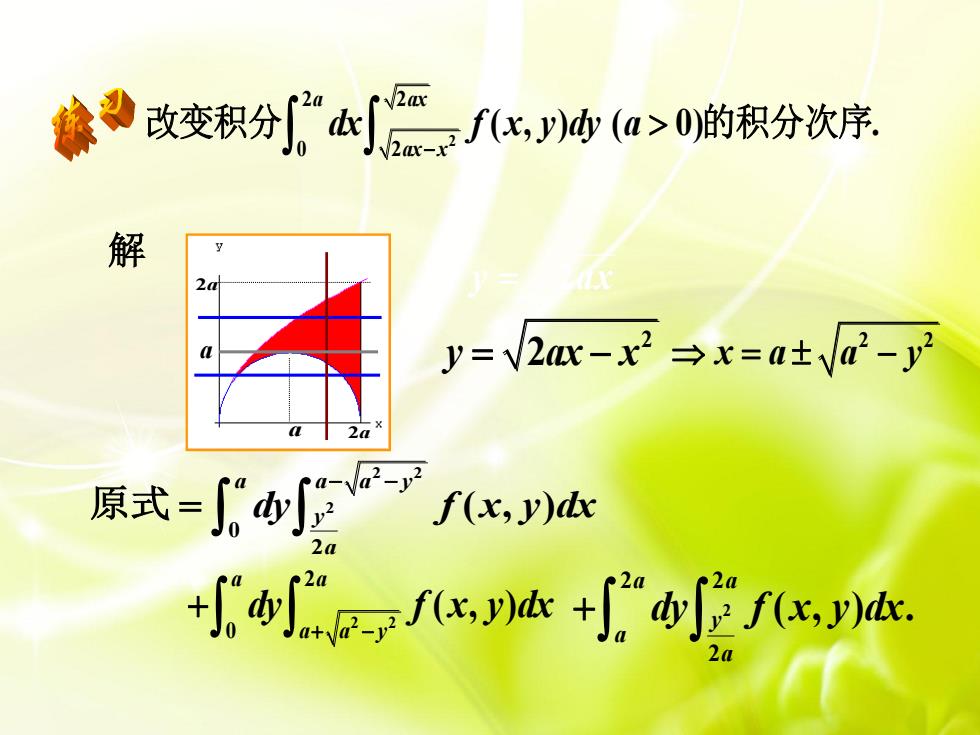
镰改变积分x海(a>0的积分次序. 解 2a y=V2ac-x2→x=a±Va2- 原式=2x, tx,+f
y 2ax 解 2 2 2 0 ( , ) a a a a y dy f x y dx 2 2 2 2 ( , ) . a a y a a dy f x y dx 2 y ax x 2 2 2 x a a y a 2a 2a a 2 2 2 0 2 ( , ) ( 0) . a ax ax x dx f x y dy a 改变积分 的积分次序 2 2 2 0 2 ( , ) a a a y y a dy f x y dx 原式