说明:(1)若积分区域既是X-型区域又是Y-型区域, 则有nfc,)dxdy y=92(x) (xydy t=wy) =920y) =afxax b 为计算方便,可选择积分序,必要时还可以交换积分序 (2)若积分域较复杂,可将它分成 若干X型域或Y型域,则 =+川+
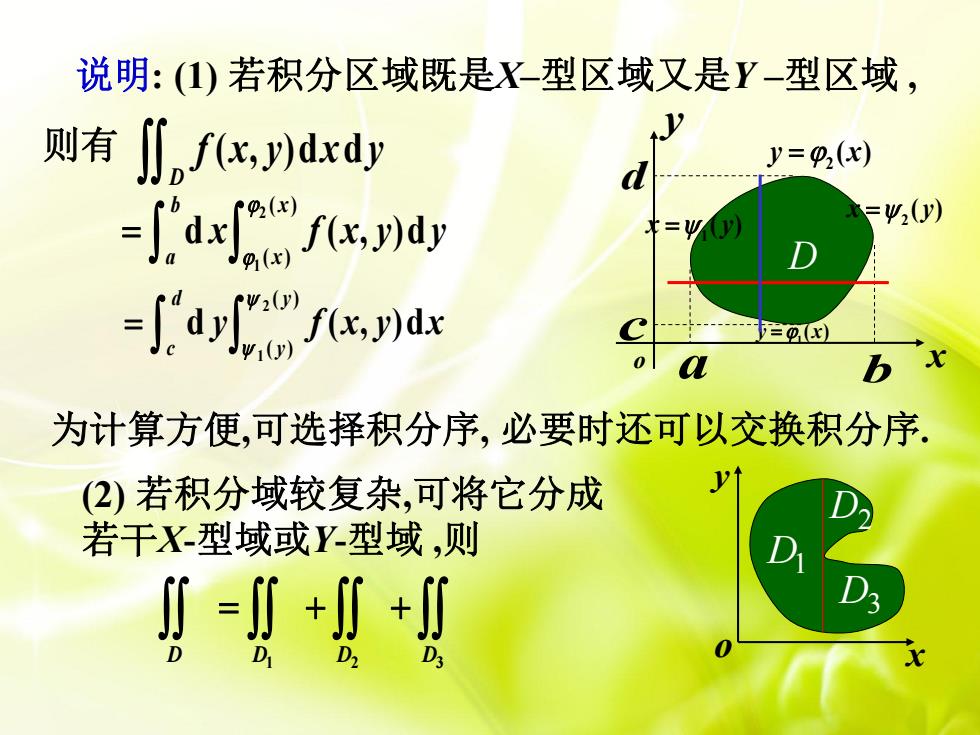
o x y 说明: (1) 若积分区域既是X–型区域又是Y –型区域 , ( , )d d D f x y x y 为计算方便,可选择积分序, 必要时还可以交换积分序. 2 y x ( ) o x y D a b 1 x y ( ) 2 x y ( ) d c 则有 1 y x ( ) 2 1 ( ) ( ) d ( , )d b x a x x f x y y 2 1 ( ) ( ) d ( , )d d y c y y f x y x (2) 若积分域较复杂,可将它分成 若干X-型域或Y-型域 ,则 D1 D2 D3 D D D D 1 2 3

利用直系计算二重积分的步骤 (1)画出积分区域的图形,求出边界曲线交点坐标; (2)根据积分域类型,确定积分次序; (3)确定积分限,化为二次定积分; (4)计算两次定积分,即可得出结果 注意:二重积分转化为二次定积分时,关键在 于正确确定积分限,一定要做到熟练、准确
注意:二重积分转化为二次定积分时,关键在 于正确确定积分限,一定要做到熟练、准确。 利用直系计算二重积分的步骤 (1)画出积分区域的图形,求出边界曲线交点坐标; (3)确定积分限,化为二次定积分; (2)根据积分域类型, 确定积分次序; (4)计算两次定积分,即可得出结果

例1.计算I=儿。ydo,其中D是直线y=1,x=2,及 y=x所围的闭区域。 解法1.将D看作X-型区域,则D: 1≤y≤x 1≤x≤2 Idxfxyax 2 y=x 金细8期■发g年年年装自 i片r-]ar 解法2.将D看作y-型区域则D:sx≤2 -可a时w=i-3小-8
x y 2 1 1 y x o 2 2 2 1 1 2 d 2 x y y y 例1. 计算 d , D I x y 其中D 是直线 y=1, x=2, 及 y=x 所围的闭区域. x 解法1. 将D看作X–型区域, 则 1 : 1 2 y x D x 2 1 1 d d x I x x y y 2 2 1 1 d 2 1 x x y x 2 3 1 1 1 d 2 2 x x x 9 8 解法2. 将D看作Y–型区域, 则 2 : 1 2 y x D y 2 2 1 d d y I y x y x 2 3 1 1 2 d 2 y y y 9 8 y

例2.计算川xydo,其中D是抛物线广=x及直线 y=x-2所围成的闭区域。 解:为计算简便,先对x后对y积分,y =X 则1 4 -1≤y≤2 -1 y=x-2 Jydc =y=0+2- -日誓
例2. 计算 d , D x y 其中D 是抛物线 所围成的闭区域. 解: 为计算简便, 先对 x 后对 y 积分, 2 2 : 1 2 y x y D y d D x y 2 2 2 1 d y y y xydx 2 2 2 2 1 1 d 2 y y x y y 2 2 5 1 1 [ ( 2) ] d 2 y y y y D 2 y x y x 2 2 1 4 o y x y 及直线 则

例3.计算 川d、其中D是直线)- 所围成的闭区域。 解:由被积函数可知,先对x积分不行, y=x X=元 因此取D为X-型域: 0≤y≤x 元 D: 0≤x≤π 灯ndd=nad =∫sinxdx=-cosx]W=2 说明:有些二次积分为了积分方便,还需注意积分顺序
例3. 计算 sin d d , D x x y x 其中D 是直线 所围成的闭区域. o x y D x 解 y x : 由被积函数可知, 因此取D 为X – 型域 : 0 : 0 y x D x sin d d D x x y x 0 sin dx x 2 0 0 sin d d x x x y x 先对 x 积分不行, 说明: 有些二次积分为了积分方便, 还需注意积分顺序