
第四节对面积的曲面积分 ·一、桡念的引入 ·二、对面积的曲面积分的定义 ·三、计算法 ·四、小结思考题
第四节 对面积的曲面积分 • 一、概念的引入 • 二、对面积的曲面积分的定义 • 三、计算法 • 四、小结 思考题
一、概念的引入 实例 若曲面Σ是光滑的,它的面密度为连 续函数p(x,y,z),求它的质量. 所谓曲面光滑即 000 曲面上各点处都有 4000 切平面,且当点在曲 面上连续移动时,切 2000 平面也连续转动. -40-200 20 40
一、概念的引入 若曲面是光滑的, 它的面密度为连 续函数( x, y,z), 求它的质量. 实例 所谓曲面光滑即 曲面上各点处都有 切平面,且当点在曲 面上连续移动时,切 平面也连续转动
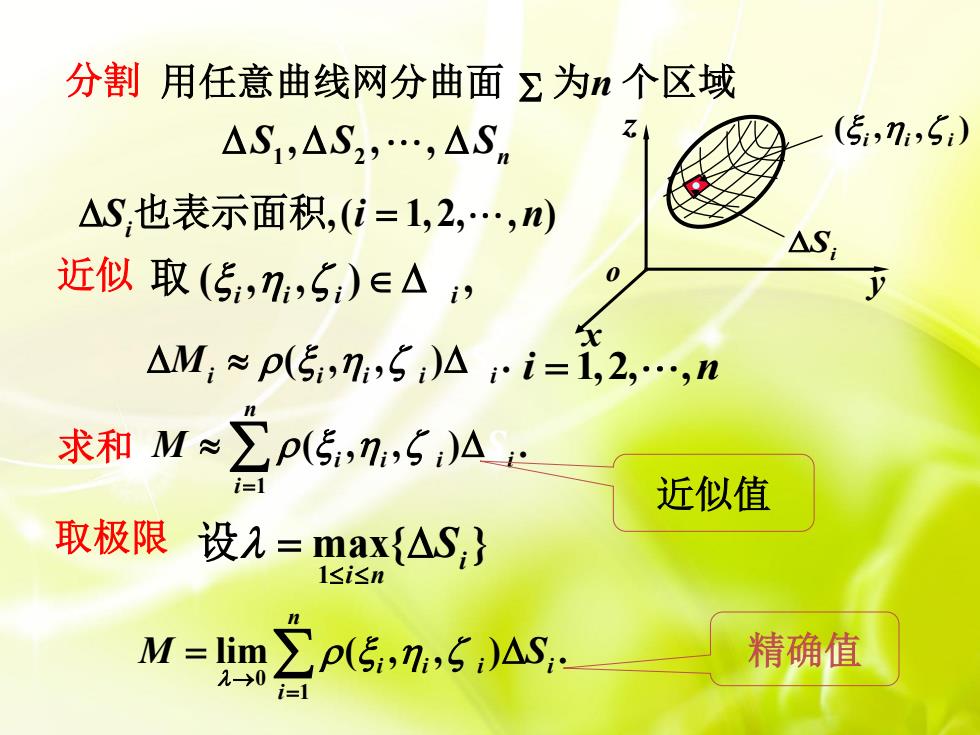
分割用任意曲线网分曲面Σ为n个区域 △S1,△S2,.,△Sn (5,17,5) △S,也表示面积,(i=1,2,.,n) △S 近似取(5,7,5)∈△i) △M1≈p(5,n,5)A-i=1,2,n 求和M≈∑p(5,n,5,)A 近似值 取极限设2=max{△S;} 1<i<n M=m2p5,m6,)△. 精确值
分割 i n 1,2, , ,( 1,2, , ) S i n i也表示面积 1 2 , , , S S Sn 用任意曲线网分曲面 为n 个区域 近似 1 ( , , ) . n i i i i i M S 近似值 ( , , ) , 取 i i i i S ( , , ) . Mi i i i i S 取极限 0 1 lim ( , , ) . n i i i i i M S 精确值 1 max{ }i i n S 设 Si ( , , ) i i i y z o x 求和

二、对面积的曲面积分的定义 定义设曲面Σ是光滑的,函数f(x,y,)在∑ 上有界,把∑分成n小块△S:(△S;同时也表示 第i小块曲面的面积),设点(5,7,5)为△S:上任 意取定的点,作乘积f(5,n,5)△S, 并作和∑f(5,7,5)·△S,如果当各小块曲面 i=1 的直径的最大值入→0时,这和式的极限存在, 则称此极限为函数f(x,y,z)在曲面∑上对面积 的曲面积分或第一类曲面积分
二、对面积的曲面积分的定义 设曲面是光滑的, 函 数 f (x, y,z)在 上有界, 把分 成n小 块Si(Si同时也表示 第i小块曲面的面积),设点( , , ) i i i 为Si上任 意取定的点,作乘积 ( , , ) i i i f Si , 并作和 n i i i i f 1 ( , , ) Si , 如果当各小块曲面 的直径的最大值 0时, 这和式的极限存在, 则称此极限为函数 f ( x, y,z)在曲面上对面积 的曲面积分或第一类曲面积分. 定义

记为 J∬fx,z)aS. 即J∬f(x,z)S=1im∑f5,n,5)As: 入→0 i=1 其中f(x,y,z)叫被积函数,叫积分曲面. 当f(x,y,z)在光滑曲线曲面Σ上连续时, 对曲面的曲面积分丁f(x,少,z)S存在 若Σ可分为分片光滑的曲面Σ,及Σ2,则 f2s=/,s+∬s
即 f (x, y,z)dS i i i n i f i S lim ( , , ) 1 0 记为 f ( x, y,z)dS. f (x, y,z)dS 1 2 f (x, y,z)dS f ( x, y,z)dS. 1 2 若 可分为分片光滑的曲面 及 , 则 其中 f x y z ( , , ) . 叫被积函数,叫积分曲面 ( , , ) , ( , , ) . f x y z f x y z dS 当 在光滑曲线曲面 上连续时 对曲面的曲面积分 存在