
第二节对坐标的曲线积分 ·一、问题的提出 ·二、对坐标的曲孩积分的橇急 ·三、对坐标的曲孩积分的计算 ·四、两美曲孩积分之同的联素 。五、小结思考题
第二节 对坐标的曲线积分 • 一、问题的提出 • 二、对坐标的曲线积分的概念 • 三、对坐标的曲线积分的计算 • 四、两类曲线积分之间的联系 • 五、小结 思考题
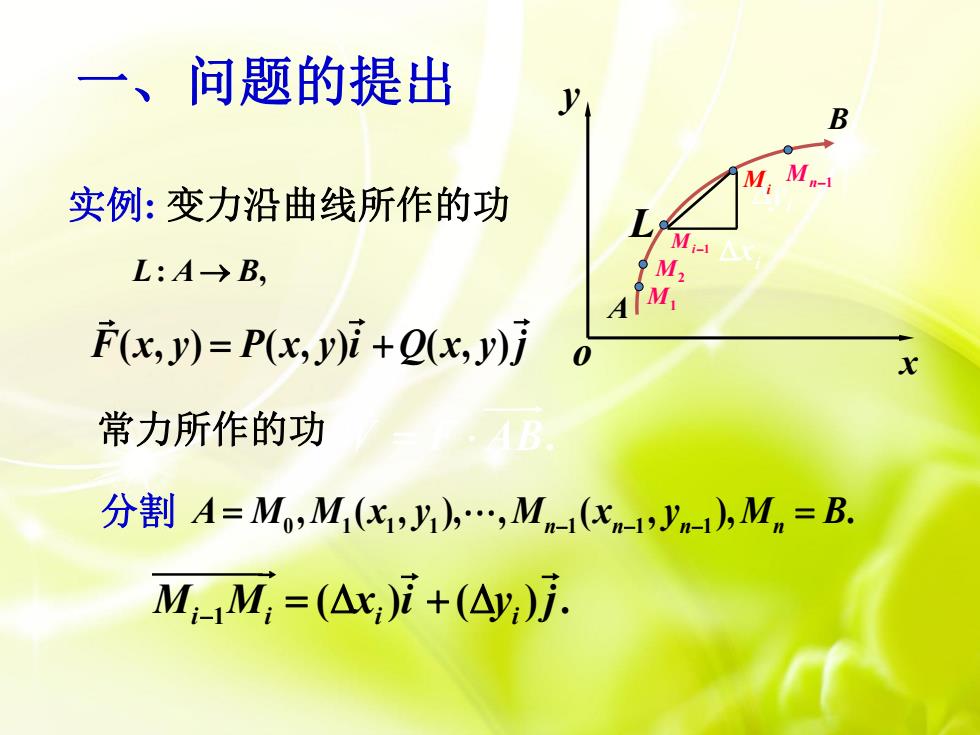
一、问题的提出 实例:变力沿曲线所作的功 L:A→B, F(x,y)=P(x,y)i+Q(x,y)j 常力所作的功 分割A=M,M(化,J),Mn-(cyMn=B. M-1M,=(△x,)i+(△y,)j:
o x y A B L Mn1 Mi1 M2 M1 i x i 实例 y : 变力沿曲线所作的功 L A B : , F x y P x y i Q x y j ( , ) ( , ) ( , ) 常力所作的功 分割 0 1 1 1 1 1 1 , ( , ), , ( , ), . A M M x y M x y M B n n n n 1 ( ) ( ) . M M x i y j i i i i W F AB . Mi 一、问题的提出
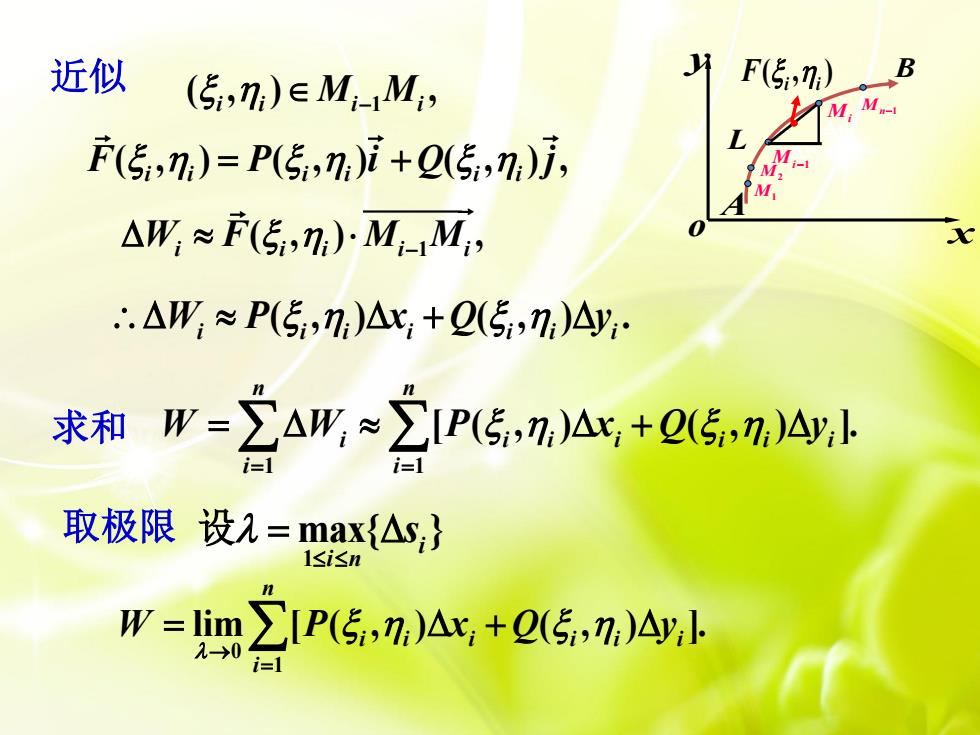
近似 (5,7)eMM, F(5,1) MM. F(5,)=P(5,n,)i+0(5,), M △W;≈F(5,n,)M1M, .△W≈P(5,;)△x,+(5,n)Ay 求和W=立A形=2IP发,nA+Q5,74l 取极限设孔=2A} ()Ax,+()
o x y B L ( , ) F i i xi i y 近似 取极限 0 1 lim [ ( , ) ( , ) ]. n i i i i i i i W P x Q y ( , ) ( , ) ( , ) , F P i Q j i i i i i i 1 ( , ) , W F M M i i i i i ( , ) ( , ) . W P x Q y i i i i i i i 1 1 [ ( , ) ( , ) ]. n n i i i i i i i i i W W P x Q y A 1 max{ }i i n s 设 1 ( , ) , i i i i M M Mn1 Mi Mi1 M2 M1 求和

二、对坐标的曲线积分的概念 1.定义 设L为xOy面内从点A到点B的一条有向光滑曲 线弧,函数P(x,y),Q(x,y)在L上有界.用L上的点 M1(x1,1),M2(x2y2),Mn-1(cm-1,yn-1)把L分成 个有向小弧段 M-1M:(i=1,2,.,店M=A,Mn=B). 设△x,=X-x-1)△y,=y,-y-1,点(5,)为M-1M 上任意取定的点.如果当各小弧段长度的最大值 元→0时
二、对坐标的曲线积分的概念 1 1 1 2 2 2 1 1 1 1 0 1 1 1 , ( , ), ( , ) . ( , ), ( , ), , ( , ) ( 1,2, , ; , ). , , ( , ) . 0 , nnn i i n i i i i i i i i i i L xoy A B P x y Q x y L L M x y M x y M x y L n M M i n M A M B x x x y y y M M 设 为 面内从点 到点 的一条有向光滑曲 线弧 函数 在 上有界 用 上的点 把 分成 个有向小弧段 设 点 为 上任意取定的点 如果当各小弧段长度的最大值 时 1.定义

∑P(5,n,)△x,的极限存在,则称此极限为函数P(x,y) 在有向曲线弧L上对坐标的曲线积分(或称第二类曲线 积分),记作 ∫P(x,y)dc=Iim∑P(5,n,)△x -0 类似地定义∫2(x,y)=1im∑0(5,7,)A i=1 其中P(化,y),Q(x,y)叫做被积函数,L叫积分弧段
1 0 1 ( , ) , ( , ) ( , ) lim ( , ) ( , . n i i i i n i i i L i P x P x y L P x y dx x P x 对坐标 的曲线 的极限存在 则称此极限为函数 在有向曲线弧 上 积分 或称第二类曲线 积分) 记作 类似地定义 0 1 ( , ) lim ( , ) . n i i i L i Q x y dy Q y 其中P x y Q x y L ( , ), ( , )叫做被积函数, . 叫积分弧段