
第四节多元复合晶数的 求导法则 ·一、链式法则 ·二、金微分形式的不变性 ·三、小结思考题
第四节 多元复合函数的 求导法则 • 一、链式法则 • 二、全微分形式的不变性 • 三、小结 思考题
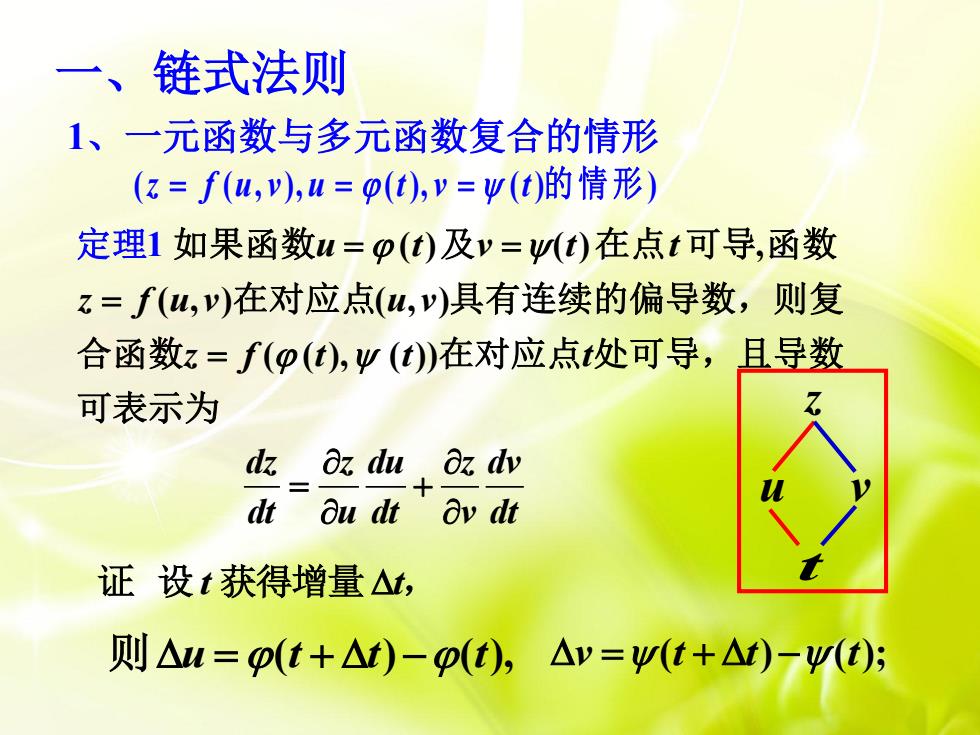
一、链式法则 1、一元函数与多元函数复合的情形 (z=f(u,),u=p(t),y=w(t)的情形) 定理1如果函数u=p(t)及y=y(t)在点t可导,函数 z=f(u,v)在对应点(u,v)具有连续的偏导数,则复 合函数z=f(p(t),业(t)在对应点处可导,且导数 可表示为 dz az du oz dv dt Ou dt t Ov dt 证设t获得增量△t 则△u=p(t+△t)-p(t),△v=V(t+△)-y(t);
证 则 u t t t ( ) ( ), v t t t ( ) ( ); 设 t t 获得增量 , 1、一元函数与多元函数复合的情形 ( ) ( ) , ( , ) ( , ) ( ( ), ( )) 1 u t v t t z f u v u v z f t t t dz z du z dv dt u dt v dt 如果函数 及 在点 可导 函数 在对应点 具有连续的偏导数,则复 合函数 在对应点 处可导,且导数 可表示为 定理 一、链式法则 z u v t ( ( , ), ( ), ( ) ) z f u v u t v t 的情形

由于函数z=f(w,v)在(w,)点具有连续的偏导数 4s9 AAv+AAv, Ou 当△u→0,△y→0时,E-→0,62→0 △zOz△u,Oz△y,。△u,。△y △tOu△t'Ov△t +61t +82 At 当△t→0时,u→0,△y→0 y血,A如 △W dv △t'dt At dt d lim △z_ozdu,zdy dt △t-→0△t Ou dt dt
1 2 , z z z u v u v u v 1 2 z z u z v u v t u t v t t t , , u du v dv t dt t dt 由于函数z f u v u v ( , ) ( , ) 在 点具有连续的偏导数 当 t u v 0 0 0 时, , 1 2 当 u v 0 0 0 0 , 时, , 0 lim . t dz z z du z dv dt t u dt v dt
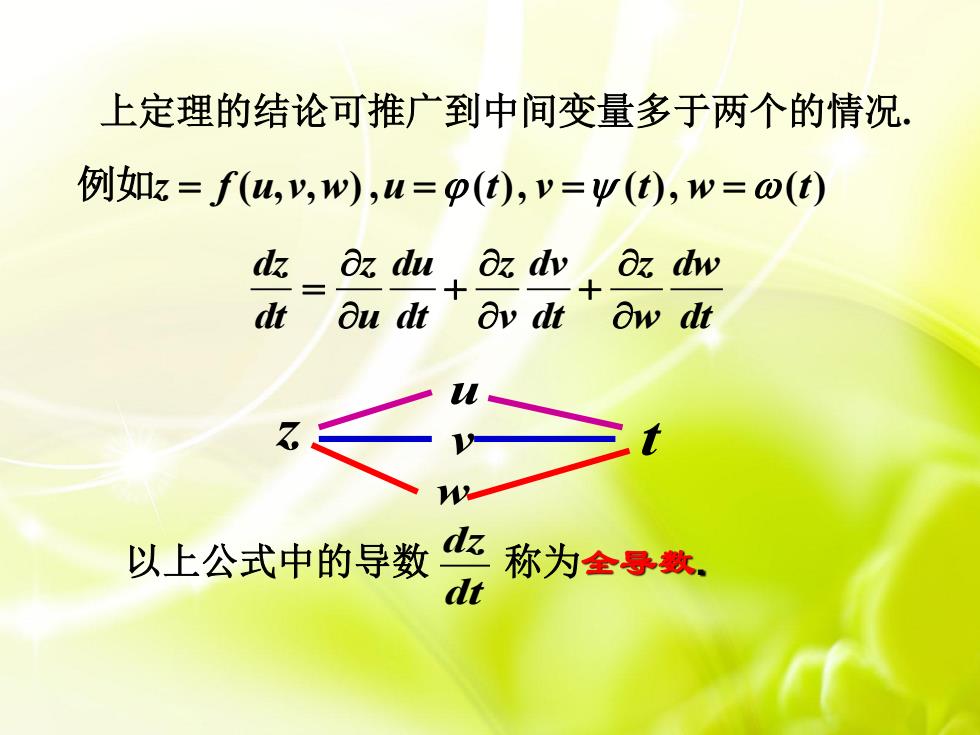
上定理的结论可推广到中间变量多于两个的情况. 例如z=f(w,y,w),u=p(),v=y(t),w=o(t) dz az du oz dy az dw dt Ou dt'Ov dt'Ow dt 以上公式中的导数 名称为金都款
上定理的结论可推广到中间变量多于两个的情况. dz z du z dv z dw dt u dt v dt w dt u v w z t 以上公式中的导数 称为全导数. dz dt 例如z f u v w u t v t w t ( , , ) , ( ), ( ), ( )

设z=w+sim6而u=e,v=cos6求全导数 dz az du oz dv az 解 dt Ou dt'Oy dt'Ot ve'-usint+cost e'cost-e'sint+cost e'(cost-sint)+cost
解 dz z du z dv z dt u dt v dt t ve u t t t sin cos e t e t t t t cos sin cos e (cost sin t) cost. t 1 sin cos . t dz z uv t u e v t dt 例 设 ,而 , ,求全导数