
第六节高斯公式通量与救度 ·一、高斯公式 ·二、简单的应用 ·三、物理意义一通量与散度 ·四、小猪思考题
第六节 高斯公式 通量与散度 • 一、高斯公式 • 二、简单的应用 • 三、物理意义—通量与散度 • 四、小结 思考题

一、高斯公式 定理1设空间闭区域Ω由分片光滑闭曲面Σ围成, 函数P(x,z八2(x,y,z小R(x,y,z)在2上具有 一阶连续的偏导数,则有公式 器器h-∯的女+Qk+a 或卯器+等+器-博rama+Qam+Ram 这里Σ是的整个边界曲面的外侧, c0sa,c0sB,cosy是Σ上点(K,y,z)处的法向量的方向余弦
一、高斯公式 ( , , ) ( , , ) ( , , ) ( ) ( ) ( cos cos cos ) cos ,cos ,cos 1 P x y z Q x y z R x y z P Q R dv Pdydz Qdzdx Rdxdy x y z P Q R dv P Q R dS x y z 设空间闭区域 由分片光滑闭曲面 围成, 函数 、 、 在 上具有 一阶连续的偏导数,则有公式 或 这里 是 的整个边界曲面的外侧 理 , 定 是上点( , , ) . x y z 处的法向量的方向余弦
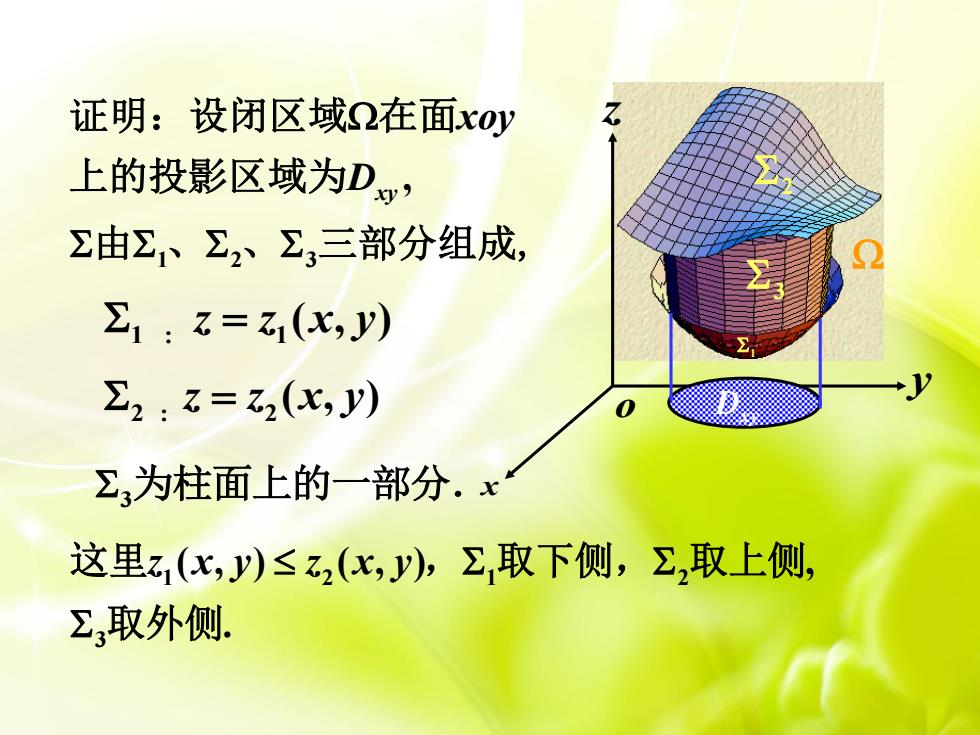
证明:设闭区域Q在面x0y 上的投影区域为D, 2由∑、22、23三部分组成, 1:z=z(x,y) ∑2:z=2(x,y) ∑3为柱面上的一部分.x 这里z(,y)≤乙,(x,y),取下侧,2,取上侧, Σ,取外侧
x y z o 1 : 1 z z x y ( , ) 2 : 2 z z x y ( , ) 1 2 3 Dxy 3 为柱面上的一部分. 1 2 3 , xy xoy D 证明:设闭区域 在面 上的投影区域为 由 、 、 三部分组成, 1 2 1 2 3 ( , ) ( , ) , . z x y z x y 这里 , 取下侧, 取上侧 取外侧

根据三重积分的计算法 亚股-a =厂{Rx,z,(x,yI -RIx,y,(x,y)hdxdy 根据曲面积分的计算法 「Rx,ak=-Rx,3,y
根据三重积分的计算法 2 1 ( , ) ( , ) { } xy z x y z x y D R R dv dz dxdy z z 2 1 { [ , , ( , )] [ , , ( , )]} Dxy R x y z x y R x y z x y dxdy 根据曲面积分的计算法 1 1 ( , , ) [ , , ( , )] , Dxy R x y z dxdy R x y z x y dxdy x y z o 1 2 3 Dxy

∬Rx,八z)=j∬Rx,a(x,yd, ∬R(x,yz)=0. 23 于是∬R(x,八z)k x,y(x,y)-RIx,y,z(x,y)dcdy, ∬-∯Rx3
2 2 ( , , ) [ , , ( , )] , Dxy R x y z dxdy R x y z x y dxdy 2 1 { [ , , ( , )] [ , , ( , )]} , Dxy R x y z x y R x y z x y dxdy R x y z dxdy ( , , ) 于是 3 R x y z dxdy ( , , ) 0. ( , , ) . R dv R x y z dxdy z