
第二节二重积分的计算 ·一、利用直角坐标计算二重积分 ·二、利用极坐标计算二重积分 ·三、小猪徐习毁
第二节 二重积分的计算 • 一、利用直角坐标计算二重积分 • 二、利用极坐标计算二重积分 • 三、小结 练习题

一、利用直角坐标系计算二重积分 如果积分区域为:p,(x)≤y≤p,(x),a≤r≤b.[X-型] yy=0(x) y59(x) y丰9x) y+9() b b七 其中函数p,(x)、p(x)在区间[4,b上连续
如果积分区域为: 1 2 ( ) ( ), . x y x a x b 其中函数 、 在区间 上连续. 1 ( ) x 2 ( ) x [ , ] a b [X-型] 一、利用直角坐标系计算二重积分 1 y x ( ) 2 y x ( ) x o b y D a 1 y x ( ) 2 y x ( ) x b o y D a
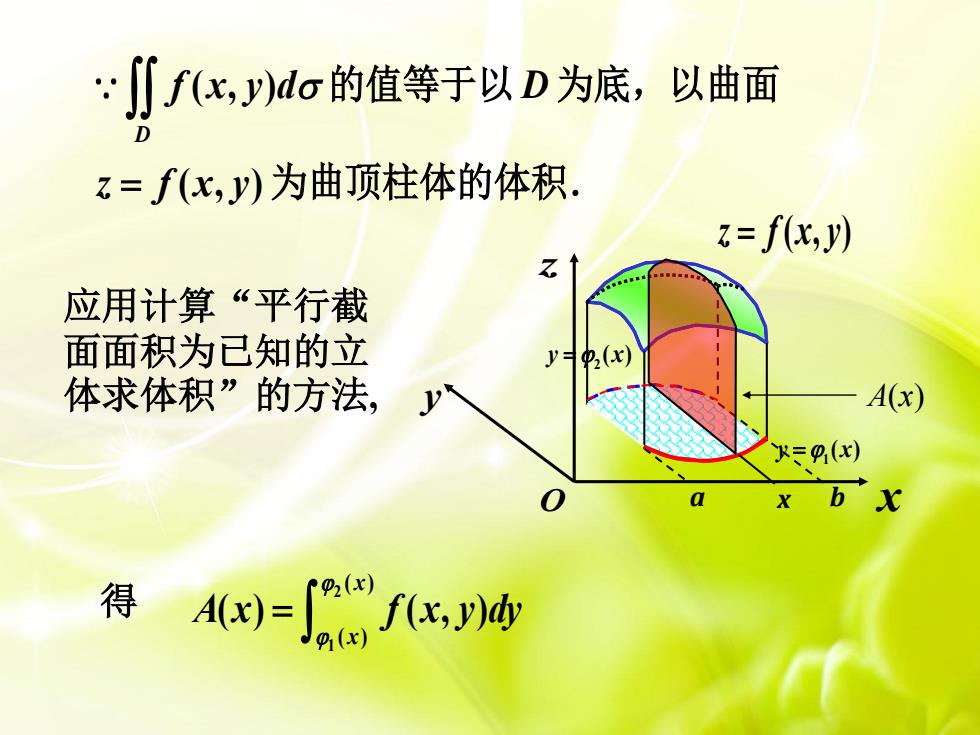
∬fc,)do的值等于以D为底,以曲面 z=f(化,y)为曲顶柱体的体积. z=f(x,y) 应用计算“平行截 面面积为已知的立 体求体积”的方法, A(x) 三9() 得=
( , ) ( , ) D f x y d D z f x y 的 值等 于 以 为底,以 曲 面 为 曲 顶柱体 的 体积. 应用计算“平行截 面面积为已知的立 体求体积”的方法 , 2 1 ( ) ( ) ( ) ( , ) xx A x f x y dy 得 z f x y ( , ) x y zO D 2 y x ( ) a x b A (x ) 1 y x ( )

于是y=JAe=fx, 则jfc)aa干f,依. 二次积分 习惯上二次积分也写作 amfc,a
二次积分 2 1 ( ) ( ) ( ) [ ( , ) ] . b b x a a x V A x dx f x y dy dx 于是 2 1 ( ) ( ) ( , ) [ ( , ) ] . b x a x D f x y d f x y dy dx 则 2 1 ( ) ( ) ( , ) b x a x dx f x y dy 习惯上二次积分也写作

如果积分区域为:)≤x≤y以,c≤y≤d. [Y-型] d x=V2(0y) x=2y) d x=v(y) D x=(y) c xa=Jxaw fca
如果积分区域为: [Y-型] 2 1 2 1 ( ) ( ) ( ) ( ) ( , ) [ ( , ) ] = ( , ) d y c y D d y c y f x y d f x y dx dy dy f x y dx 1 2 ( ) ( ), . y x y c y d x d o y c 1 x y ( ) 2 x y ( ) D y 1 x y ( ) 2 x y ( ) x d o c