
第、节多元强教的极值及其求法 一、二元高数的极值和最值 二、条件极值拉格朗日乘赵法 三、小结
第八节 多元函数的极值及其求法 一、二元函数的极值和最值 二、条件极值拉格朗日乘数法 三、小结

一、多元函数的极值和最值 观察二元函数z=- e的图形 x
一、多元函数的极值和最值 观察二元函数 x 2 y 2 的图形 e x y z

1、二元函数极值的定义 定义设函数z=f(x,y)的定义域为D,P(xo,) 为D的内点,若存在P的某邻域U(P)cD,使得 对于该邻域内异于P的任何点(x,y),都有 f(x,y)<f(xo,Yo), 则称函数f(x,y)在点(x,)有极大值f(x,y) 点(x,y)为函数f(x,y)的极大值点
1、二元函数极值的定义 000 0 0 0 ( , ) , ( , ) ( ) ( , ), z f x y D P x y D P U P D P x y 设函数 的定义域为 为 的内点,若存在 的某邻域 ,使得 对于该邻域内异于 的任何点 定义 都有 0 0 0 0 0 0 0 0 ( , ) ( , ), ( , ) ( , ) ( , ) ( , ) ( , ) f x y f x y f x y x y f x y x y f x y 则称函数 在点 有极大值 , 点 为函数 的极大值点

若对于该邻域内异于P的任何点(x,y),都有 f(x,y)>f(xo,Yo), 则称函数f(x,y)在点(x,)有极小值f(xo,y) 点(x,y)为函数f(x,y)的极小值点. 极大值、极小值统称为极值。 使函数取得极值的点称为极值点
0 0 0 0 0 0 0 0 0 ( , ), ( , ) ( , ), ( , ) ( , ) ( , ) ( , ) ( , ) P x y f x y f x y f x y x y f x y x y f x y 若对于该邻域内异于 的任何点 都有 则称函数 在点 有极小值 , 点 为函数 的极小值点. 极大值、极小值统称为极值. 使函数取得极值的点称为极值点
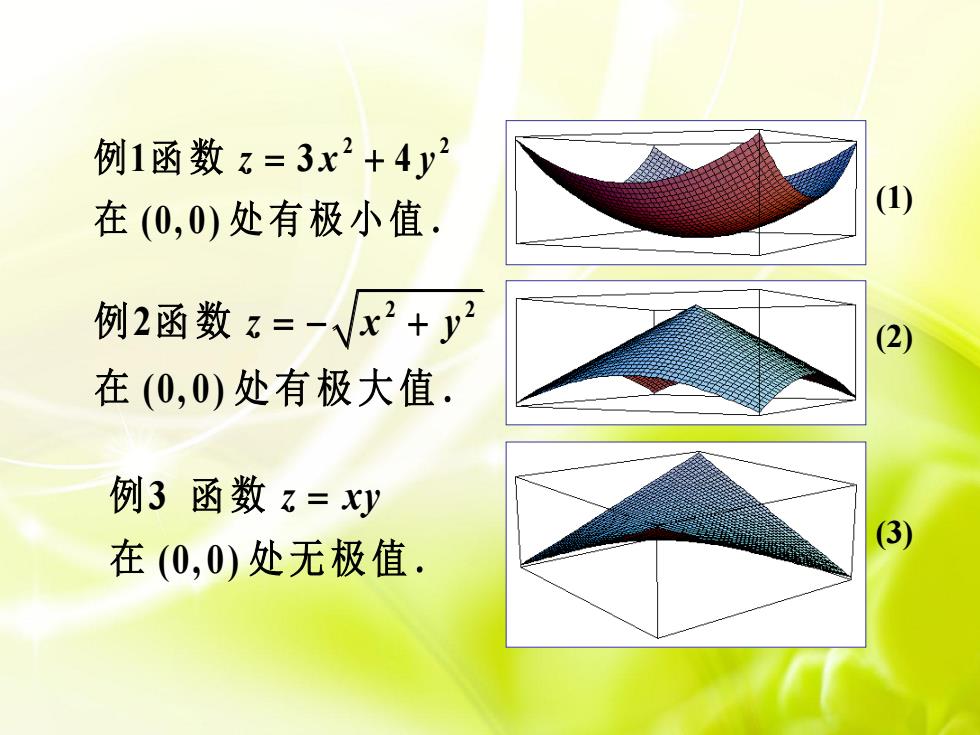
例1函数z=3x2+4y2 在(0,0)处有极小值, (1) 例2函数z=-√x2+y2 (2) 在(0,0)处有极大值. 例3函数z=xy 3) 在(0,0)处无极值
(1) (2) (3) 2 2 1 3 4 (0, 0) 例 函 数 z x y 在 处 有 极 小 值. 2 2 2 (0, 0) 例 函 数 z x y 在 处 有 极 大 值. 3 (0, 0) 例 函 数 z xy 在 处 无 极 值 .