《高等数学》课程教学资源（课件讲稿）第十一章_11.7 斯托克斯公式 环流量与旋度

第七节斯托克斯公式环流量与旋度 ·一、斯花克斯公式 ·二、简单应用 ·三、物理意义一环流量与旋度 ·四、小结 思考题

第七节 斯托克斯公式 环流量与旋度 • 一、斯托克斯公式 • 二、简单应用 • 三、物理意义—环流量与旋度 • 四、小结 思考题

一、斯托克斯(stokes)公式 定理1设厂为分段光滑的空间有向闭曲线，Σ是 以T为边界的分片光滑的有向曲面，Γ的正向与 Σ的侧符合右手规则，函数P(x,y,z),2(x,y,z), R(x,y,z)在包含曲面2在内的一个空间区域内具 有一阶连续的偏导数，则有公式 器+ axkc+( =∮Pk+Q+Rd 斯托克斯公式

一、斯托克斯(stokes)公式 斯托克斯公式 ( , , ), ( , , ), ( , , ) ( ) ( 1 ) ( ) P x y z Q x y z R x y z R Q P R Q P dydz dzdx dxdy y z z x x y Pdx Qdy Rdz                               设 为分段光滑的空间有向闭曲线， 是 以 为边界的分片光滑的有向曲面， 的正向与 的侧符合右手规则，函数 在包含曲面 在内的一个空间区域内具 有一阶连续的偏导数，则有公式 定理

便于记忆形式 dydz dzdx dxdy 0 0 ay Ox =∮nP+O+Rk P 2 R 另一种形式 cosa cos B cosy 0 0 Ox ay Ox S=∮Pc+O+Rdk P Q R 其中i={cosa,cosB,c0sy}

dydz dzdx dxdy Pdx Qdy Rdz x y z P Q R              cos cos cos dS Pdx Qdy Rdz x y z P Q R                 另一种形式 n  {cos,cos  ,cos }  其中 便于记忆形式

Stokes公式的实质： 表达了有向曲面上的曲面积分与其边界曲线 上的曲线积分之间的关系. (当Σ是xoy面的平面闭区域时) 斯托克斯公式 特殊情形 格林公式

Stokes公式的实质: 表达了有向曲面上的曲面积分与其边界曲线 上的曲线积分之间的关系. 斯托克斯公式 特殊情形 格林公式 (当Σ 是xoy面的平面闭区域时)

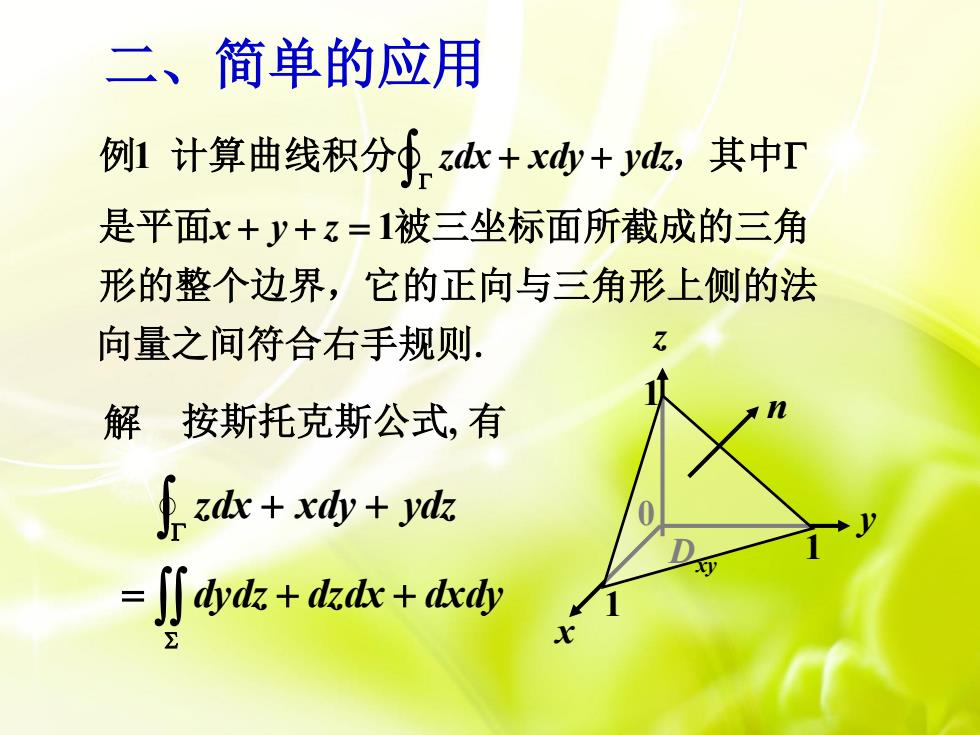
二、简单的应用 例1计算曲线积分∮z+x+y,其中T 是平面x+y+z=1被三坐标面所截成的三角 形的整个边界，它的正向与三角形上侧的法 向量之间符合右手规则. 解按斯托克斯公式，有 手zd+x+ydk =j小yd+dkdc+dcdy

二、简单的应用 解 按斯托克斯公式, 有 zdx xdy ydz       dydz  dzdx  dxdy Dxy x y z n 1 1 1 0 1 1 zdx xdy ydz x y z        例 计算曲线积分 ，其中 是平面 被三坐标面所截成的三角 形的整个边界，它的正向与三角形上侧的法 向量之间符合右手规则