《线性代数》课程教学课件（PPT讲稿，B）第二章 矩阵与向量_2-3 向量组的线性相关性

线性代数 山东理工大学

线性代数 山东理工大学

第2章矩阵与向量 §2.3 向量组的线性相关性 ●向量的线性组合 ·向量组的线性相关、线性无关 ·向量组的等价 ●向量组的秩 ·向量空间的基

§2.3 向量组的线性相关性 第2章 矩阵与向量 ● 向量的线性组合 ● 向量组的线性相关、线性无关 ● 向量组的等价 ● 向量组的秩 ● 向量空间的基

1.向量的线性组合 定义1： 对于向量组，1,2，L,0m,如果有一组数 入1，元2，L,元m,使C=九C1+22+L+九nmm 称为向量a是向量a1,2,L,am一个线性组 合，或称&可由a1,a2,L,aCm线性表示

1. 向量的线性组合 定义1： 对于向量组 1 2 , , , , ,     L m 如果有一组数    1 2 , , , , L m 使        = + + + 1 1 2 2 L m m 称为向量 是向量 一个线性组 合，或称  可由 1 2 , , ,    L m 线性表示。  1 2 , , ,    L m

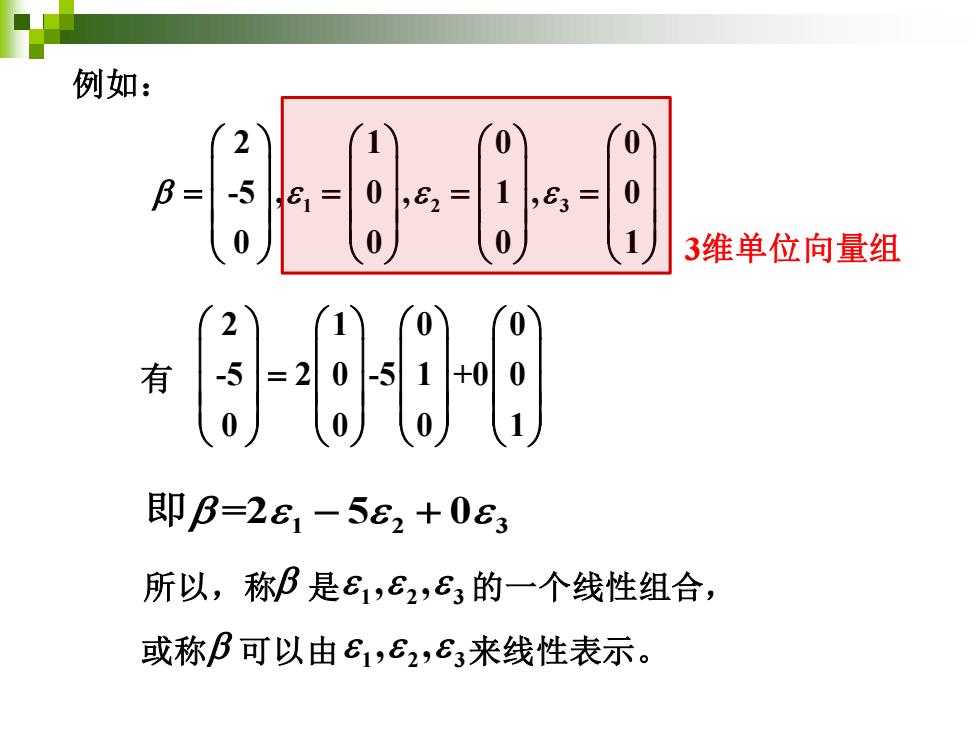
例如： 72 1 0 0) B= -5 81= 0 ,82= 1 ,83= 0 0 0 0 3维单位向量组 2 1 0 0 有 -5 =2 0 -5 1 +00 0 0 即B=261-562+083 所以，称B是81,82,83的一个线性组合， 或称B可以由81,82,83来线性表示

例如： 1 2 3 2 1 0 0 -5 , 0 , 1 , 0 0 0 0 1                     = = = =                         有 2 1 0 0 -5 2 0 -5 1 +0 0 0 0 0 1                 =                         即    =2 5 0 1 2 3 − + 所以，称  是    1 2 3 , , 的一个线性组合， 3维单位向量组  1 2 3 或称 可以由    , , 来线性表示

例1证明向量B=(0,4,2)是向量01=(1,2,3)，c2=(2,3,1), a=(3,1,2)的线性组合，并将B用1，a2,a,线性表示。 解假定B=a1+2,2+入，a3,即 1 2 3 2+2 + 04 3 1 由向量的相等，得 2+222+323=0, 22+3九2+23=4， 32+九2+223=2

1 2 3 1 2 3 (0,4,2) (1,2,3), (2,3,1), (3,1,2) , ,         = = = = 例1 证明向量 是向量 的线性组合，并将 用 线性表示。 1 1 2 2 3 3 解 假定       = + + ,即 1 2 3 1 2 3 1 2 3 2 3 0, 2 3 4, 3 2 2.           + + =   + + =  + + =  由向量的相等,得 1 2 3 1 2 3 0 2 3 1 4 3 1 2 2                    + + =                        