《线性代数》课程教学课件（PPT讲稿，B）第四章 线性方程组_4-1 线性方程组解的判别

线性代数 山东理工大学

线性代数 山东理工大学

第4章线性方程组 。内容提要 §4.1线性方程组解的判别 §4.2齐次线性方程组 §4.3非齐次线性方程组

第4章 线性方程组 ◼ 内容提要 §4.1 线性方程组解的判别 §4.2 齐次线性方程组 §4.3 非齐次线性方程组

第4章线性方程组 §4.1线性方程组的判别

§4.1 线性方程组的判别 第4章 线性方程组

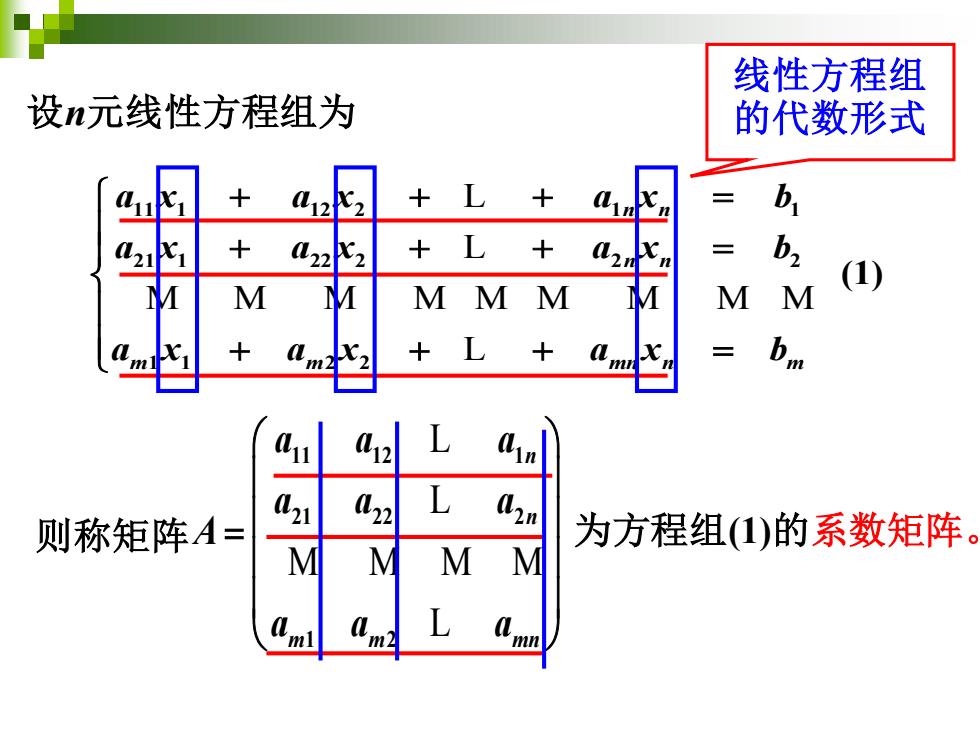
线性方程组 设n元线性方程组为 的代数形式 21 + L b2 (1) M M M M M M M M 十 L 12 L 021 022 则称矩阵A= 为方程组()的系数矩阵 M M M L

设n元线性方程组为 11 1 12 2 1 1 21 1 22 2 2 2 1 1 2 2 (1) n n n n m m mn n m a x a x a x b a x a x a x b a x a x a x b  + + + =   + + + =     + + + = L L M M M M M M M M M L 则称矩阵 11 12 1 21 22 2 1 2 n n m m mn a a a a a a A a a a     =         L L M M M M L 为方程组(1)的系数矩阵。 线性方程组 的代数形式

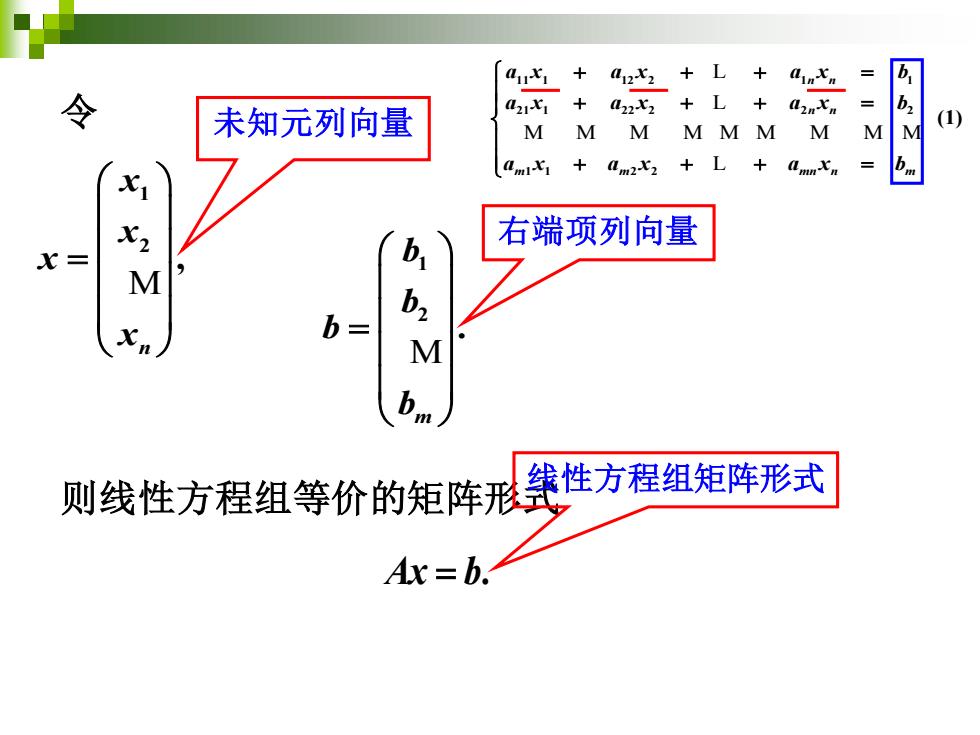
022+L = b 未知元列向量 021水1+ × = (1) M MM MMM M M amiX1 am2x2+L amnXn 右端项列向量 M b= b M 则线性方程组等价的矩阵形线性方程组矩阵形式 Ax=b

令 1 2 , n x x x x     =         M 则线性方程组等价的矩阵形式 Ax b = . 1 2 . m b b b b     =         M 未知元列向量 右端项列向量 线性方程组矩阵形式 11 1 12 2 1 1 21 1 22 2 2 2 1 1 2 2 (1) n n n n m m mn n m a x a x a x b a x a x a x b a x a x a x b  + + + =   + + + =     + + + = L L M M M M M M M M M L