
线性代数 山东理工大学
线性代数 山东理工大学

第1章n阶行列式 §1.4克拉默(Gramer)法则
§1.4 克拉默(Gramer)法则 第1章 n阶行列式

引入行列式概念时,求解二、三元线性方程组,当系数 列式D≠0时,方程组有唯一解,飞 (i=1,2,3) 对(1-3)式表示的元线性方程组 411X1+412X2+L+41mXm=b1, 211+a22X2+L+2mXn=b2, (1.5) LLLLLLLLLL anx+an2x2+L +amnxn=bn 其未知量的系数构成的行列式 au an L ain 021 22L D= 02n 称为方程组的系数行列式 LLLLLLL anl
D 0 = (i = 1,2,3) D D x i i 引入行列式概念时,求解二、三元线性方程组,当系数 行列式 时,方程组有唯一解, 对(1-3)式表示的n元线性方程组 其未知量的系数构成的行列式 称为方程组的系数行列式 11 12 1 21 22 2 1 2 n n n n nn a a a a a a D a a a = L L LLLLLLL L (1.5) . 11 1 12 2 1 21 1 22 2 2 2 1 1 2 2 n n n n n n nn n n a x a x a x b a x a x a x b a x a x a x b + = + = + = LLLLLLLLL L L L L 1 , , + + + + + +

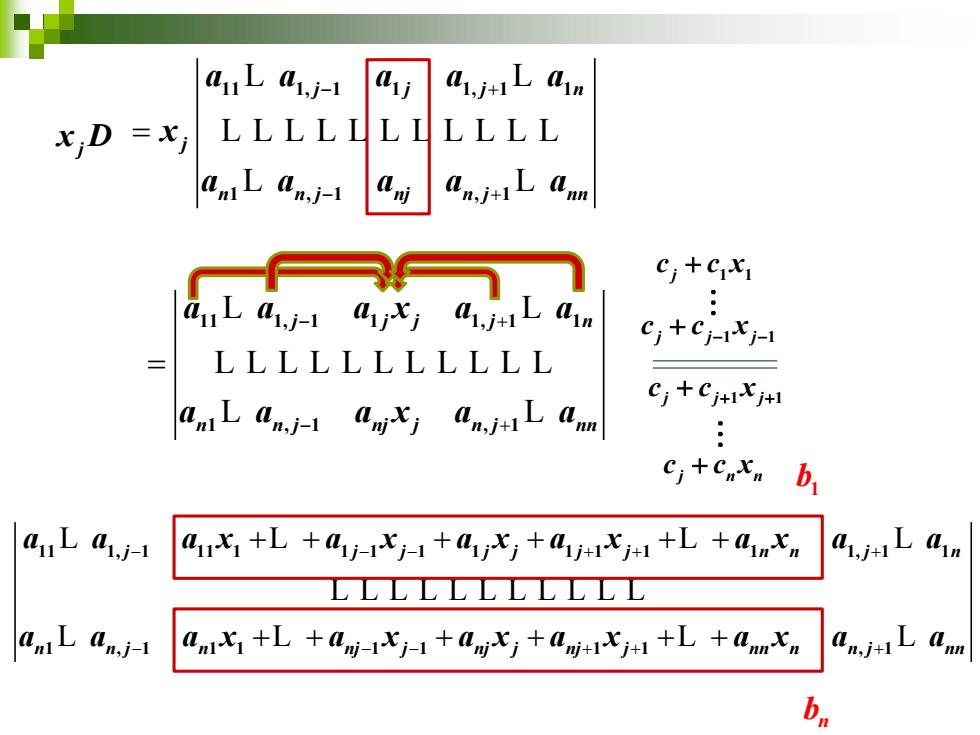
定理1.4.1(Gramer法则)如果线性方程组(1.5)的系数行列式 D≠0,则方程组(1.5)有唯一的解,且 1= 其中D,是把系数行列式D中第j列的元素用方程组右端 的常数项代替后所得到的阶行列式,即 41La1,j-1 b 41,j+L41n D= LL LLLLI LLLL amLan,j- ansLam 证明:
定理1.4.1(Gramer法则)如果线性方程组(1.5)的系数行列式 D 0, 则方程组(1.5)有唯一的解,且 1 2 3 1 2 3 , , , , . n n D D D D x x x x D D D D = = = = L 其中 是把系数行列式 中第 列的元素用方程组右端 的常数项代替后所得到的 阶行列式,即 Dj D j n 11 1, 1 1 1, 1 1 1 , 1 , 1 j j n j n n j n n j nn a a b a a D a a b a a − + − + = L L LLLLLLLLLLL L L 证明:
auL aj- aitL ain x D =xj LLLLLLLLLLL amL anj- anjLam ci+cxi ci+cj-xj-1 LLLLLLLLLLL ci+ci+x amL anj-1 anixi anitiL am : ci+cnxn b auL aj- 41x1+L+41j-xj-1+01x,+01j1xj1+L+a1nxm 工工工工工工工工工工 amL anj- amx+anjx1+anjx+an+L+amxm b
j x D 11 1, 1 1 1, 1 1 1 , 1 , 1 j j j n j n n j nj n j nn a a a a a x a a a a a − + − + = L L LLLLLLLLLLL L L j 1 1 c c x + 11 1, 1 1 1, 1 1 1 , 1 , 1 j j j j n n n j nj j n j nn a a a x a a a a a x a a − + − + = L L LLLLLLLLLLL L L 11 1, 1 11 1 1 1 1 1 1 1 1 1 1, 1 1 1 , 1 1 1 1 1 1 1 , 1 j j j j j j j n n j n n n j n nj j nj j nj j nn n n j nn a a a x a x a x a x a x a a a a a x a x a x a x a x a a − − − + + + − − − + + + + + + + + + + + + + + + L L L L LLLLLLLLLLL L L L L 1 b n b j j j 1 1 c c x + − − j j j 1 1 c c x + + + j n n c c x +