题号 二 四 总分 得分 8、二次型f,5,5=2+3++25+2,是正定的,则:的取值范围 得分☐一、选择题(本题共4小题,每小题4分,满分16分。 每小题给出的四个选项中,只有一项符合题目要求) 得分☐三、计算题(本题共2小题,每题8分,满分16分) 1、设A,B为n阶方阵,满足等式4B=0,则必有() +x11 )A=0或B=0:)4+B=0;(C)4=0或=0;(D)4+=0。 11-x11 2、A和B均为n阶矩库,且(A+B=2+2AB+B,则必有() ()A=E(⑧)B=E:(C)A=B. ()AB=B4, 3、设4为m×n矩阵,齐次方程组杠=0仅有零解的充要条件是( ()A的列向量线性无关; (⑧)A的列向量线性相关; (C)A的行向量线性无关: ()A的行向量线性相关, 4、n阶矩阵4为奇异矩阵的充要条件是() )A的秩小于: ()4≠0: ()A的特征值都等于零:)A的特征值都不等于零: 得分☐二、填空题(本题共4小题,每题4分,满分16分) 5、若4阶矩阵A的行列式4=-5,r是A的伴随矩阵,则中一。 6、A为mxm阶矩阵,且4?-A-2E=0,则(4+2E= 10、计算n阶行列式 第1页共7页
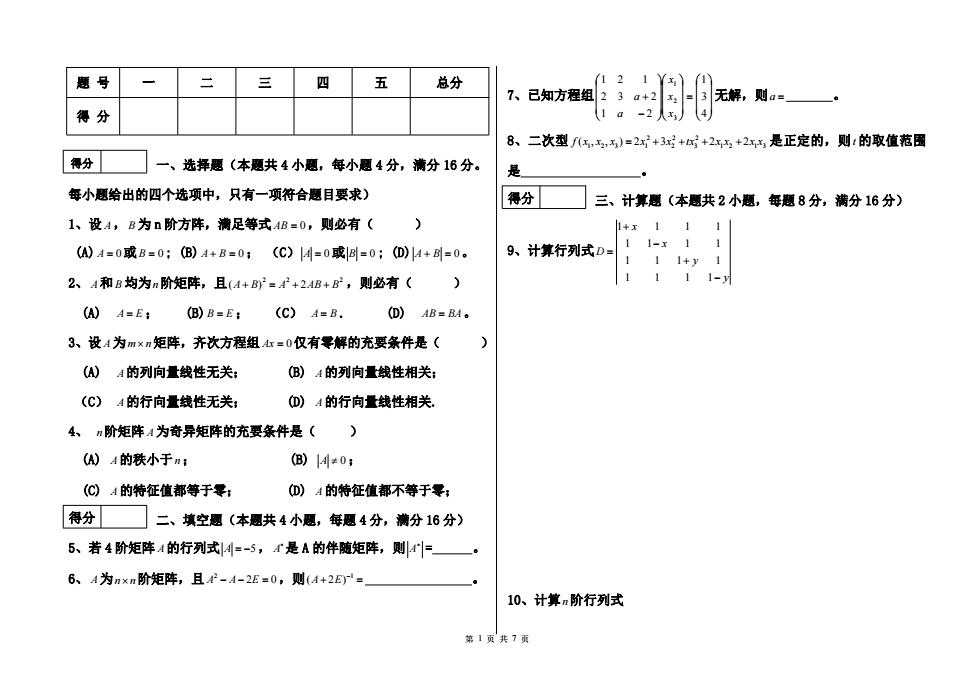
第 1 页 共 7 页 题 号 一 二 三 四 五 总分 得 分 一、选择题(本题共 4 小题,每小题 4 分,满分 16 分。 每小题给出的四个选项中,只有一项符合题目要求) 1、设 A,B 为 n 阶方阵,满足等式 AB 0,则必有( ) (A) A 0或B 0 ; (B) A B 0; (C) A 0或 B 0 ; (D) A B 0。 2、 A和B 均为n阶矩阵,且 2 2 2 (A B) A 2AB B ,则必有( ) (A) A E ; (B) B E ; (C) A B . (D) AB BA。 3、设 A为m n矩阵,齐次方程组 Ax 0仅有零解的充要条件是( ) (A) A的列向量线性无关; (B) A的列向量线性相关; (C) A的行向量线性无关; (D) A的行向量线性相关. 4、 n阶矩阵 A为奇异矩阵的充要条件是( ) (A) A的秩小于n; (B) A 0; (C) A的特征值都等于零; (D) A的特征值都不等于零; 二、填空题(本题共 4 小题,每题 4 分,满分 16 分) 5、若 4 阶矩阵 A的行列式 A 5, A 是 A 的伴随矩阵,则 A = 。 6、 A为n n阶矩阵,且 2 A A 2E 0,则 1 (A 2E) 。 7、已知方程组 4 3 1 1 2 2 3 2 1 2 1 3 2 1 x x x a a 无解,则a 。 8、二次型 2 2 2 1 2 3 1 2 3 1 2 1 3 f (x , x , x ) 2x 3x tx 2x x 2x x 是正定的,则t 的取值范围 是 。 三、计算题(本题共 2 小题,每题 8 分,满分 16 分) 9、计算行列式 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 x x D y y 10、计算n阶行列式 得分 得分 得分
+3 11、若向量组a,a,a,线性相关,向量组a,a,a,线性无关。证明: D.= (1)a,能有a,a3钱性表出: (2)a,不能由a,a,a,线性表出。 12、设A是n阶矩方阵,E是n阶单位矩阵,A+E可逆,且 fA)=(E-A(E+4A)-。 证明 (1)(E+f(AE+A)=2E: (2)ff4)=A。 得分☐四、证明题(本题共2小题,每小题8分,满分16分。 写出证明过程) 第2页共7页
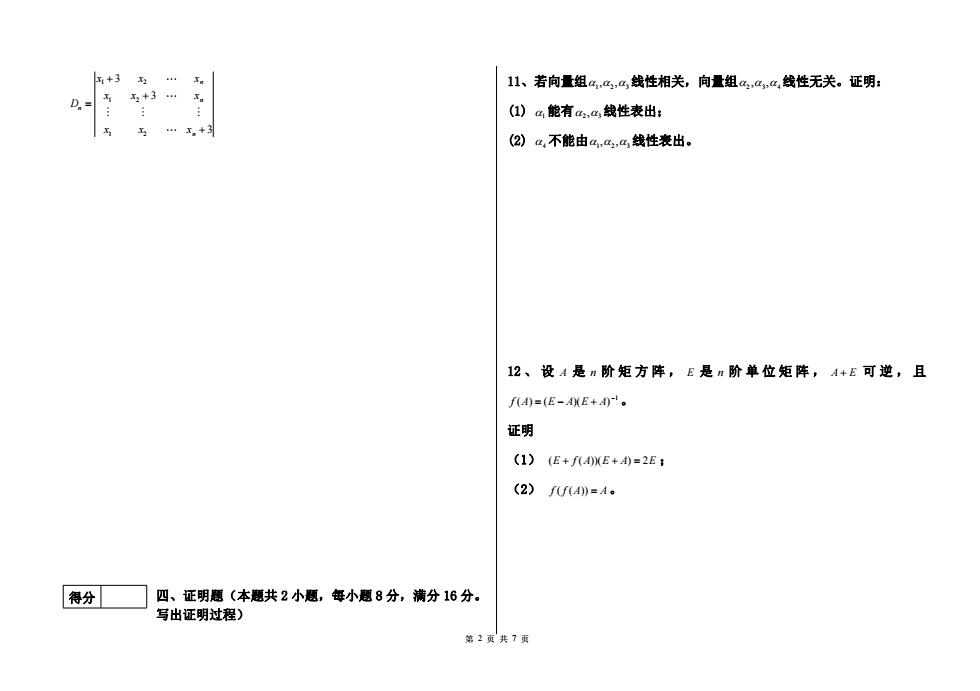
第 2 页 共 7 页 1 2 1 2 1 2 3 3 3 n n n n x x x x x x D x x x 四、证明题(本题共 2 小题,每小题 8 分,满分 16 分。 写出证明过程) 11、若向量组 1 2 3 , , 线性相关,向量组 2 3 4 , , 线性无关。证明: (1) 1能有 2 3 , 线性表出; (2) 4不能由 1 2 3 , , 线性表出。 12 、 设 A 是 n 阶 矩 方 阵 , E 是 n 阶 单 位 矩 阵 , A E 可 逆 , 且 1 f (A) (E A)(E A) 。 证明 (1) (E f (A))(E A) 2E ; (2) f ( f (A)) A。 得分

得分五、解答题(本愿共3小题,每小愿12分,满分32分。 解答应写出文字说明或演算步骤) (200 13、设A=032,求一个正交矩阵P使得P4P为对角矩阵。 023 工1+3+=0 14、已知方程组{x+2x:+m1=0与方程组x+2x+3=a-1有公共解。 +4:+a2x3=0 求a的值。 第3页共7或
第 3 页 共 7 页 五、解答题(本题共 3 小题,每小题 12 分,满分 32 分。 解答应写出文字说明或演算步骤) 13、设 2 0 0 0 3 2 0 2 3 A ,求一个正交矩阵P 使得 1 P AP 为对角矩阵。 14、已知方程组 4 0 2 0 0 3 2 1 2 1 2 3 1 2 3 x x a x x x ax x x x 与方程组 2 1 x1 x2 x3 a 有公共解。 求a的值。 得分
1 3 4 求该方程组的通解。 15、设四元非齐次线性方程组的系数矩阵的秩为3,已知m,2,是它 的三个解向量,且 第4页共7页
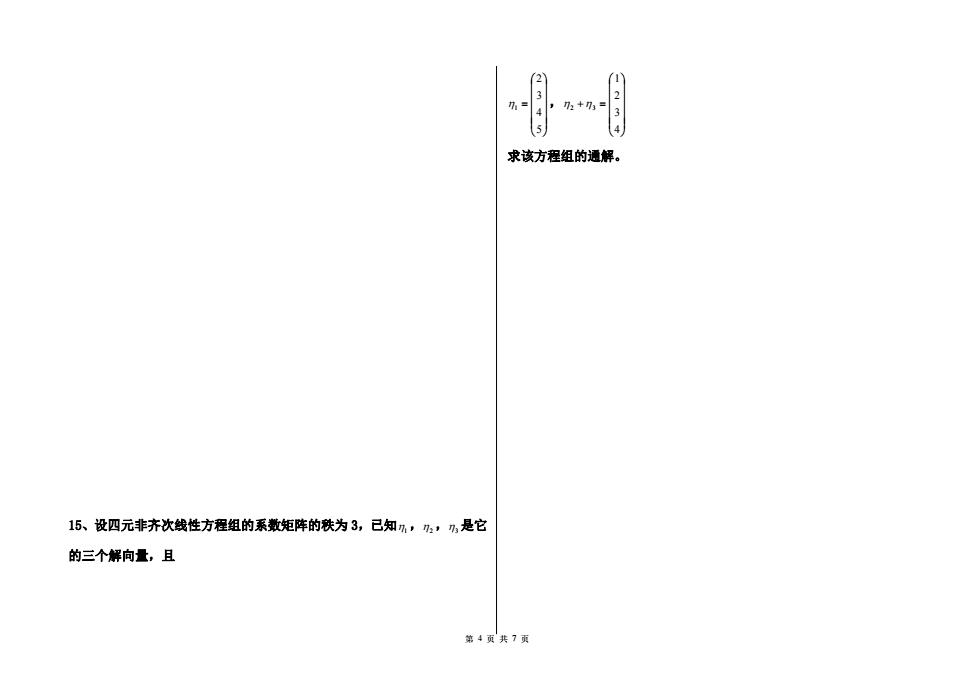
第 4 页 共 7 页 15、设四元非齐次线性方程组的系数矩阵的秩为 3,已知1, 2,3是它 的三个解向量,且 5 4 3 2 1 , 4 3 2 1 2 3 求该方程组的通解

解答和评分标准 一、选择恩 1、C: 2、Ds 3、A: 4、A. 10、解:把各列加到第一列,然后提取第一列的公因子三+3小再通 二、填空题 过行列式的变换化为上三角形行列式 5、-125: 6、: 7、-1: 8心 三、计算题 (4分) 9、解:第一行减第二行,第三行减第四行得: 12x。+3 x x 00 13x.x 11-x11 3 0 D= o 0 yy h111- 003 第二列减第一列,第四列减第三列得: (4分) 000 D= -x10 四、证明题 (4分) 00y0 101- 11、证明: 按第一行展开得 (1)、因为a:,a,a,线性无关,所以a,a线性无关。, 又aa,a,线性相关,故a能由a,a,线性表出。 (4分) ra1,马a)=3, 按第三列展开得 (2)、(反正法)若不,则a能由a,a,a,钱性表出, 不妨设a,=k,+ka,+k3· (4分) 由(1)知,g,能由1,a线性表出, 第5页共7页
第 5 页 共 7 页 解答和评分标准 一、选择题 1、C; 2、D; 3、A; 4、A。 二、填空题 5、-125; 6、 2 ; 7、-1; 8、 5 3 t 。 三、计算题 9、解:第一行减第二行,第三行减第四行得: 0 0 1 1 1 1 0 0 1 1 1 1 x x x D y y y 第二列减第一列,第四列减第三列得: 0 0 0 1 1 0 0 0 0 1 0 1 x x D y y (4 分) 按第一行展开得 1 0 0 0 0 1 x D x y y 按第三列展开得 2 2 0 1 x D xy x y y 。 (4 分) 10、解:把各列加到第一列,然后提取第一列的公因子 n i i x 1 3 ,再通 过行列式的变换化为上三角形行列式 2 2 1 2 1 1 3 3 1 3 n n n n i i n x x x x D x x x (4 分) 2 1 1 0 3 0 3 0 0 3 n n i i x x x 1 1 3 3 n n i i x (4 分) 四、证明题 11、证明: (1)、 因为 2 3 3 , , 线性无关,所以 2 , 3线性无关。, 又1 , 2 , 3线性相关,故1 能由 2 , 3 线性表出。 (4 分) 1 2 3 r( , , ) 3 , (2)、(反正法)若不,则 4能由 1 2 3 , , 线性表出, 不妨设 4 11 2 2 3 3 k k k 。 由(1)知,1 能由 2 , 3线性表出