
第五章相似矩阵与二次型 第一节 向量的阳积及正交向量组
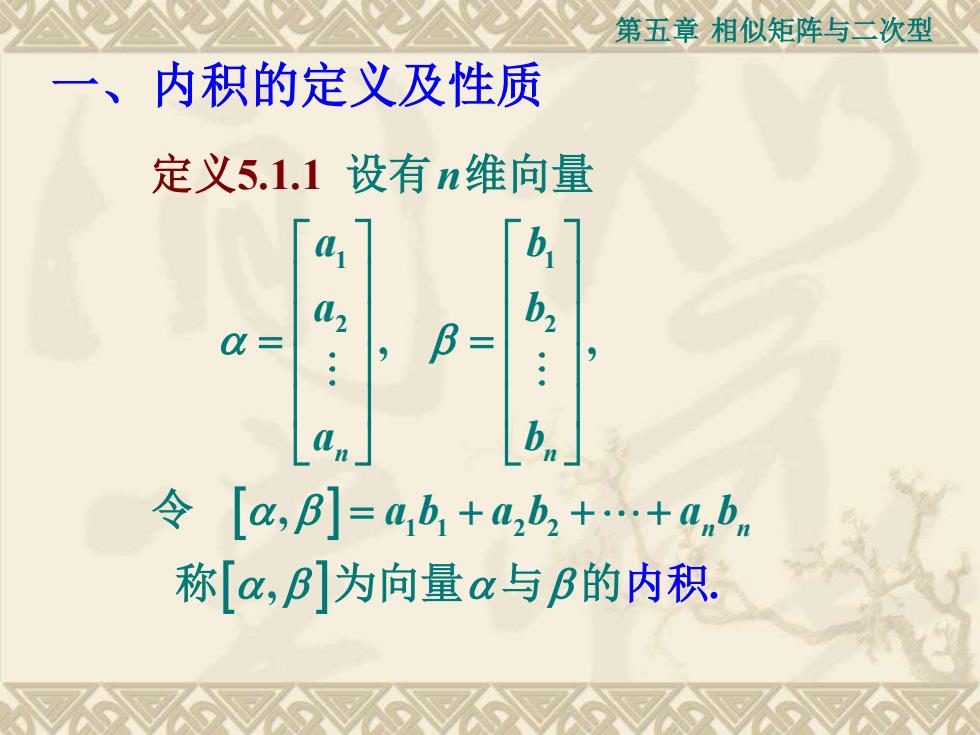
第五章 相似矩阵与二次型 第一节 向量的内积及正交向量组
第五章相似矩阵与二次型 一、 内积的定义及性质 定义5.1.1设有n维向量 42 b2 = B= .: b 令[a,B]=ab1+ub2+.+anbn 称[a,B]为向量x与B的内积
第五章 相似矩阵与二次型 1 1 2 2 1 1 2 2 , , , , 5.1.1 . n n n n n a b a b a b a b a b a b = = = + + + 设有 维向量 令 称 为向量 与 定 的内积 义 一、内积的定义及性质

第五章相似矩阵与二次型 内积的运算性质 a,B]=aa++abn (其中a,B,y为n维向量,为实数): [aB]=[B,a]; (2)[a,B]=[a,B]: (3)[a+B,r]=[a,r]+[B,y]: (4)[a,a]≥0,且当a≠0时有a,a>0
第五章 相似矩阵与二次型 内积的运算性质 (其中 , , , : 为n维向量 为实数) (1) , , ; = (2) , , ; = (3) , , , ; + = + (4) [ , ] 0, 0 [ , ] 0. 且当 时有 1 1 2 2 , n n = + + + a b a b a b

第五章相似矩阵与二次型 二、向量的长度及性质 定义5.12非负数√[a,a=√++.+称为向量 a的长度(或范数),记作a 向量的长度具有下述性质: 1.非负性当a≠0时,a>0;当a=0时,a=0; 2.齐次性2a=2‖la; 3.三角不等式la+l≤a+Bl:
第五章 相似矩阵与二次型 定义5.1.2 2 2 2 1 2 , . n a a a 非负数 = + + + 称 长度(或范数 量 的 ) 为向 ,记作 向量的长度具有下述性质: 1. 0 , 0; 0 , 0; 非负性 当 = = 时 当 时 2. ; 齐次性 = 3. . 三角不等式 + + 二、向量的长度及性质

第五章相似矩阵与二次型 若ag=1,则称a为单位向量 如果a≠0,由长度的概念得 就是一个单位向量, 用非零数 乘以向量得到一个与a同方向的 单位向量,通常称为把向量a单位化. 当la≠0,Bl≠0时,B=arccos [a,] aB 称为n维向量a与B的夹角
第五章 相似矩阵与二次型 若 = 1, . 则称 为单位向量 1 0, . 如果 由长度的概念得 就是一个单位向量 1 . 用非零数 乘以向量 得到一个与 同方向的 单位向量,通常称为把向量 单位化 , 0, 0 , arccos n . 当 = 时 称为 维向量 与 的夹角