
常微分方程数值解 Euler法与修正的Euler法 误差分析 Range--Kutta公式
1 Euler法与修正的Euler法 误差分析 Range-Kutta公式 常微分方程数值解

Euler法与修正的Euler法 一阶常微分方程初值问题: =f(x,y),xxo dx 其中,y=yK)是未知函数, y(xo)=yo 右端函数x,y)是已知函数,初值y是已知数据。 数值方法一取定离散点:x<X1<2<…<Xy 求未知函数y(x)在离散点处的近似值 y1,Jy2,y3,…,yN y :f(x,y) dx ynti-yn=f(xn,yn) h 2
2 一阶常微分方程初值问题: 0 0 0 ( ) ( , ), y x y f x y x x dx dy 数值方法——取定离散点: x0 < x1 < x2 < ··· < xN 其中, y = y(x) 是未知函数, 右端函数 f(x, y )是已知函数, 初值 y0 是已知数据。 求未知函数 y(x) 在离散点处的近似值 y1 , y2 , y3 , ·····, yN ( , ) 1 n n n n f x y h y y f ( x , y ) dx dy Euler法与修正的Euler法

求解常微分方程初值问题的Euler方法 取定步长:h,记xn=xo+nh,(n=1,2,…,N) 称计算格式:y+1=ym+hxn,yn)为Euler公式。 对应的求初值问题数值解的方法称为Euler?方法。 例2用Euler法求初值问题 =y-y2,0<x<2 x 的数值解。 y(0)=1 解:记fc,y)=y一xy2,xm=nh (n=0,1,2,…,W) 由Euler公式得: yn+i =yn+h(yn-xnyn2) (n=0,1,…,N) 3
3 求解常微分方程初值问题的Euler方法 取定步长: h,记 xn = x0 + nh, ( n = 1,2, ···, N ) 称计算格式: yn+1 = yn + h f( xn , yn ) 为Euler公式。 对应的求初值问题数值解的方法称为Euler方法。 例2 用Euler法求初值问题 (0 ) 1 , 0 2 2 y y xy x dx dy 的数值解。 解: 记 f (x, y) = y- x y 2 , xn = nh (n = 0, 1, 2,···, N ) 由Euler公式得: yn+1 = yn + h( yn- xn yn 2 ) (n = 0, 1, ···,N)
取步长h=2/10,2/20,2/30,2/40,用Euler法求解 的数值实验结果如下. N 10 20 30 40 h 0.2 0.1 0.0667 0.05 误差 0.1059 0.0521 0.0342 0.0256 2 1.5 o0 1 解析解: 0.5 1 0 0 2 3 5 y(x)= x-1+2e-x 0 数值解 准确解 4
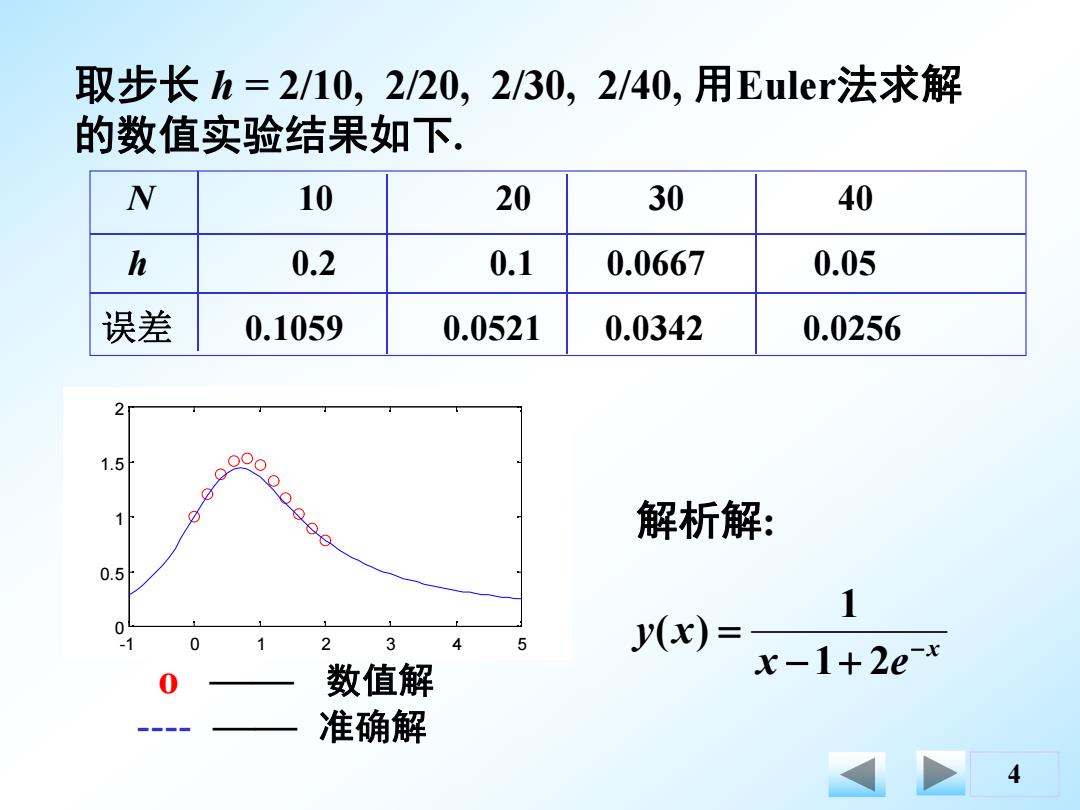
4 取步长 h = 2/10, 2/20, 2/30, 2/40, 用Euler法求解 的数值实验结果如下. N 10 20 30 40 h 0.2 0.1 0.0667 0.05 误差 0.1059 0.0521 0.0342 0.0256 x x e y x 1 2 1 ( ) 解析解: -1 0 1 2 3 4 5 0 0.5 1 1.5 2 o —— 数值解 ---- —— 准确解

用数值积分方法离散化常微分方程 y'=f(化,y) →y'(x)=f(x,(x)c x)-(x)=∫fx,y(x)d 左矩形公式 fx,Jx)kef(x,y) yn+i-yn=hf (xn2yn) 梯形公式: ,x经)+fml 2 a1-J.=2f(x,.)+fc141l
5 y’ = f (x, y) 1 ( ) ( ) ( , ( )) 1 n n x x y xn y xn f x y x dx [ ( , ) ( , )] 2 ( , ( )) 1 1 1 n n n n x x f x y f x y h f x y x dx n n 梯形公式: ( , ) n 1 n n n y y hf x y 左矩形公式 ( , ( )) ( , ) 1 n n x x f x y x dx hf x y n n 用数值积分方法离散化常微分方程 1 1 ( ) ( , ( )) n n n n x x x x y x dx f x y x dx [ ( , ) ( , )] 2 n1 n n n n1 n1 f x y f x y h y y