
数值积分 >数值积分基本概念 >插值型求积公式 >求积分的蒙特卡罗方法 >复合求积公式 >高斯型数值求积公式 >龙贝格外推计算公式
1 Ø数值积分基本概念 Ø插值型求积公式 Ø求积分的蒙特卡罗方法 Ø复合求积公式 Ø高斯型数值求积公式 Ø龙贝格外推计算公式 数值积分
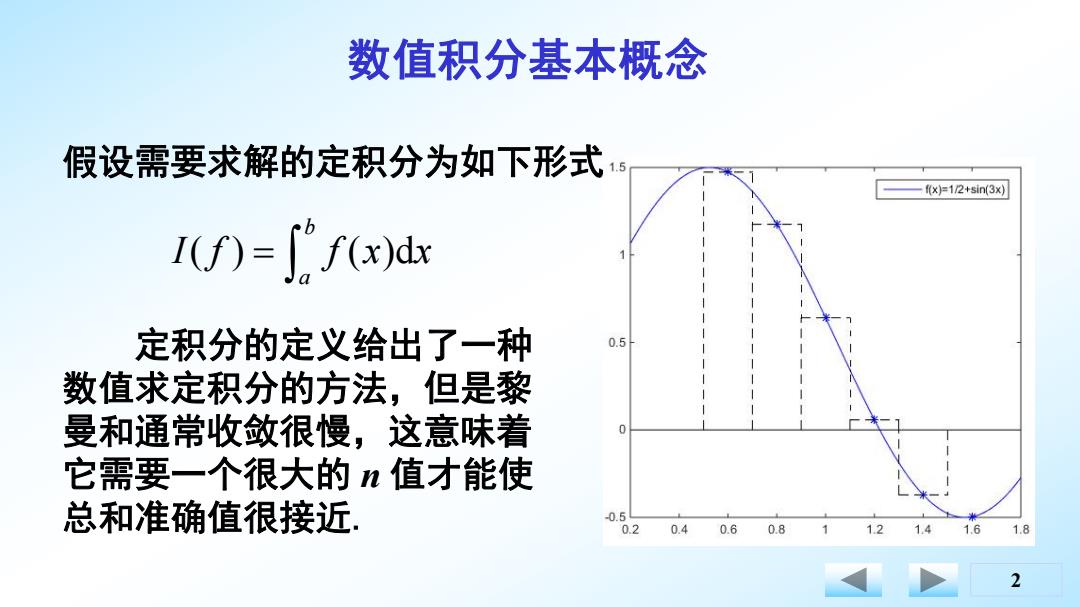
数值积分基本概念 假设需要求解的定积分为如下形式 5 f(x)=12+sin(3x) I(f)["f(x)dx 定积分的定义给出了一种 0.5 数值求定积分的方法,但是黎 曼和通常收敛很慢,这意味着 0 它需要一个很大的n值才能使 总和准确值很接近, -0.59 0.20.4 0.60.8 12 1.4
2 假设需要求解的定积分为如下形式: ( ) ( )d b a I f f x x 定积分的定义给出了一种 数值求定积分的方法,但是黎 曼和通常收敛很慢,这意味着 它需要一个很大的 n 值才能使 总和准确值很接近. 数值积分基本概念

定积分与积分和式 假设需要求解的定积分为如下形式: If)=∫fx)dx 为了找到能够尽可能逼近()准确值的数值方法.通常,求 定积分近似值的形式为 I,(f)=∑wf(x) i=lo 3
3 定积分与积分和式 假设需要求解的定积分为如下形式: ( ) ( )d b a I f f x x 为了找到能够尽可能逼近I(f)准确值的数值方法. 通常,求 定积分近似值的形式为 0 ( ) n n i i i i I f w f x

数值求积公式的一般形式 ∫f(x)=∑Asf(x)+Rf1 k=0 RU 1— 数值求积公式余项 七09七1)…,七n— 求积结点 A,A1,…,An求积系数
4 数值求积公式的一般形式 ( ) ( ) [ ] 0 f x dx A f x R f n k k k b a R[f ] —— 数值求积公式余项 x0 , x1 , ···, xn —— 求积结点 A0 , A1 , ···, An —— 求积系数
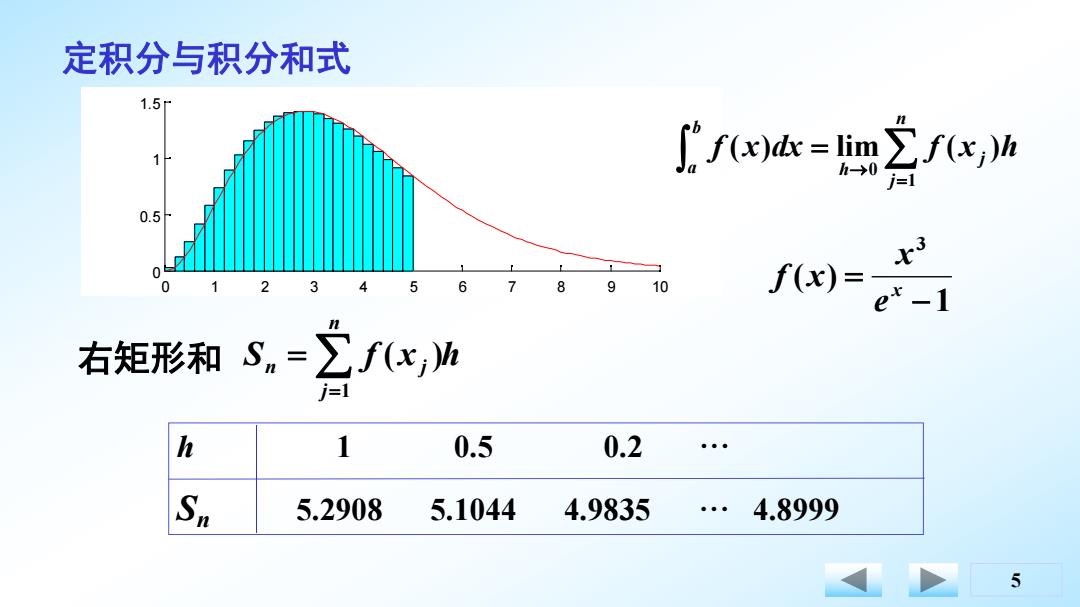
定积分与积分和式 1.5r f=2fc,h i= 0.5 x3 5 6 7 8 10 f(x)= e'-1 右矩形和S。=∑f(x,h i=1 h 1 0.5 0.2 Sn 5.2908 5.1044 4.9835 …4.8999 5
5 0 1 2 3 4 5 6 7 8 9 10 0 0.5 1 1.5 S f x h n j n j 1 ( ) 定积分与积分和式 n j j h b a f x dx f x h 1 0 ( ) lim ( ) 右矩形和 h 1 0.5 0.2 ··· Sn 5.2908 5.1044 4.9835 ··· 4.8999 1 ( ) 3 x e x f x