
敫理方程与特殊函致 第二章定解问题与偏微分方程理论(一) 主讲:杨春
第二章 定解问题与偏微分方程理论(一) 主讲:杨春

主要内容 一、波动方程 二、边界条件与初始条件
主要内容 一、波动方程 二、边界条件与初始条件

本章将学习定解问题与偏微分方程理论。 一、波动方程 (一)细弦横振动方程 波动方程是一类典型的数学物理方程,许多物理问题,如细弦振动、细杆振动、 高频传输线的电流与电压、一定条件下的电磁波等,都涉及所谓的波动方程。我 们要求认识波动方程,能够用一定方法求解部分波动方程定解问题。 下面通过两端固定的细弦振动模型导出最简单的一维齐次波动方程。 1、物理背景 一根均匀柔软的细弦线,一端固定在坐标原点,另一端沿x轴拉紧固定在x轴上 的L处,受到扰动,开始沿x轴(平衡位置)上下作微小横振动(细弦线上各点运动 方向垂直于x轴)。试建立细弦线上任意点位移函数u(x,t)所满足的规律。 30000000000008eeee9e0000000000000000000000000g
本章将学习定解问题与偏微分方程理论。 (一) 细弦横振动方程 波动方程是一类典型的数学物理方程,许多物理问题,如细弦振动、细杆振动、 高频传输线的电流与电压、一定条件下的电磁波等,都涉及所谓的波动方程。我 们要求认识波动方程,能够用一定方法求解部分波动方程定解问题。 下面通过两端固定的细弦振动模型导出最简单的一维齐次波动方程。 1、物理背景 一根均匀柔软的细弦线,一端固定在坐标原点,另一端沿x轴拉紧固定在x轴上 的L处,受到扰动,开始沿x轴(平衡位置)上下作微小横振动(细弦线上各点运动 方向垂直于x轴)。试建立细弦线上任意点位移函数u(x,t)所满足的规律。 一、波动方程
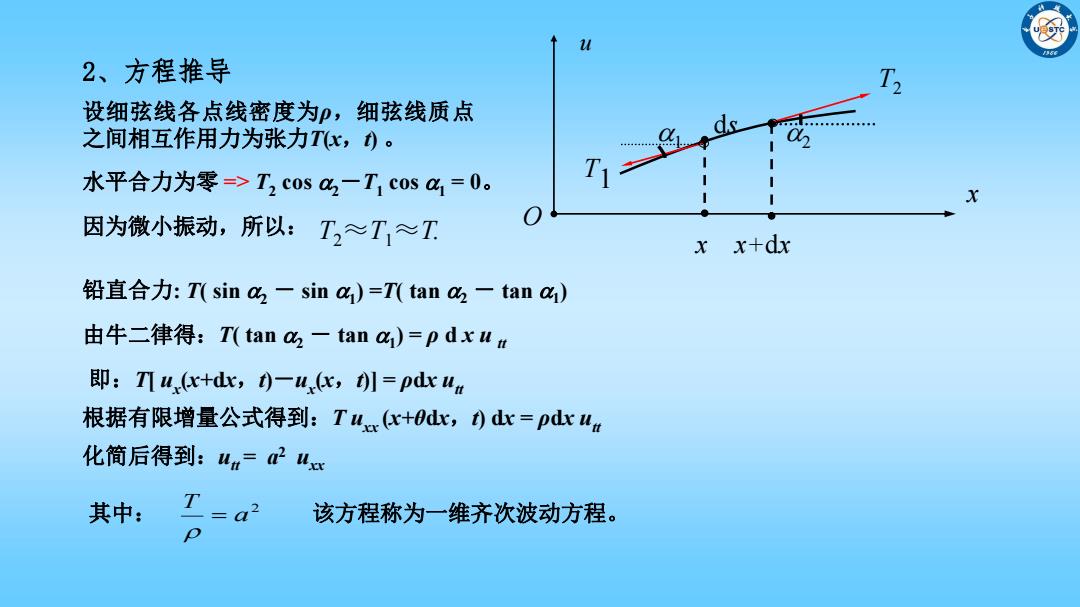
2、方程推导 设细弦线各点线密度为P,细弦线质点 之间相互作用力为张力Tx,)。 水平合力为零=>T2c0s%2-T1c0sa,=0。 T X 因为微小振动,所以:T,≈T≈T xx+dx 铅直合力:T(sin2-sin4)=T(tan必一tan) 由牛二律得:T(tan2-tana)=pdxu 即:Tux+dc,)-uc,t=pdx un 根据有限增量公式得到:Tua(c+dr,)dr=pdx uu 化简后得到:um=2ue 其中: =a2 该方程称为一维齐次波动方程。 p
2、方程推导 设细弦线各点线密度为ρ,细弦线质点 之间相互作用力为张力T(x,t) 。 u x T1 T2 O x x+dx ds 1 2 水平合力为零 => T2 cos 2-T1 cos 1 = 0。 因为微小振动,所以: T2 ≈T1 ≈T. 铅直合力: T( sin 2 - sin 1 ) =T( tan 2 - tan 1 ) 由牛二律得:T( tan 2 - tan 1 ) = ρ d x u tt 即:T[ ux (x+dx,t)-ux (x,t)] = ρdx utt 根据有限增量公式得到:T uxx (x+θdx,t) dx = ρdx utt 化简后得到:utt = a 2 uxx 其中: 2 a T 该方程称为一维齐次波动方程
2 如果要考虑细弦重量和外力作用,那么 可以导出方程形式为: uy aug+f(x,t) X xx+dx 如果还要考虑细弦受到的阻尼,那么,方程中还会包含阻尼项。 波动方程二维与三维形式为: 4=d2[u.+n]+fx,y0 4,=d2[4+4y+4e]+f,y2,)
如果要考虑细弦重量和外力作用,那么 可以导出方程形式为: u x T1 T2 O x x+dx ds 1 2 2 ( , ) tt xx u a u f x t 如果还要考虑细弦受到的阻尼,那么,方程中还会包含阻尼项。 波动方程二维与三维形式为: 2 + ( , , ) tt xx yy u a u u f x y t 2 + ( , , , ) tt xx yy zz u a u u u f x y z t