
恃征值与恃征向量的计算 。3.1.1盖氏圆 求Ax=2x ·定义3.1-1设A=[ailrn, 称由不等式lk-a≤a,所 确定的复区域为A的第i行个盖氏圆,记为G: G,=:k-ausag,i=12,...n. ·定理3.1-1若元为A的特征值,则∈UG 1
1 • 3.1.1 盖氏圆 • 定义3.1-1 设 A = [aij]nn,称由不等式 所 确定的复区域为 A 的第 i 行个盖氏圆,记为 Gi: • 定理3.1-1 若 为 A 的特征值,则 1 n ii ij j j i z a a 1 { : } 1 2 . n i ii ij j j i G z z a a i n , ,,, 1 n i i G 特征值与特征向量的计算 求Ax x

1 0.1 0.2 0.3 0.5 3 0.1 0.2 例1估计方阵特征值的范围 A= 1 0.3 0.5 0.2 -0.3 -0.1 -4 解: G1={z:lz-1s0.6};G2={z:z-3≤0.8}; G3={z:z+1≤1.8};G4={z:lz+4≤0.6}。 注:定理称A的n个特征值全落在n个盖氏圆上,但 未说明每个圆盘内都有一个特征值。 2
2 1 0.1 0.2 0.3 0.5 3 0.1 0.2 1 0.3 1 0.5 0.2 0.3 0.1 4 A G1 G2 G3 G4 例1 估计方阵特征值的范围 解: G1 = {z:|z – 1| 0.6};G2 = {z:|z – 3| 0.8}; G3 = {z:|z + 1| 1.8};G4 = {z:|z + 4| 0.6}。 注:定理称 A 的 n 个特征值全落在 n 个盖氏圆上,但 未说明每个圆盘内都有一个特征值

§1: 幂法和反幂法 设矩阵Λ=2),用特征方程容易求得4的两个 引例 特征值为 2=-1,九2=3. 取初始向量x0)=(1,0)T,计算向量序列 xk+1)=Axk),k=0,1, 具体结果如下表所示: 3
3 §1 幂法和反幂法 引例 1 2 A 2 1 取初始向量 x(0) = (1,0)T,计算向量序列 ( 1 ) ( ) , 0 1 k k x A x k , , ... 具体结果如下表所示: 设矩阵 ,用特征方程容易求得 A 的两个 特征值为 1 2 1, 3
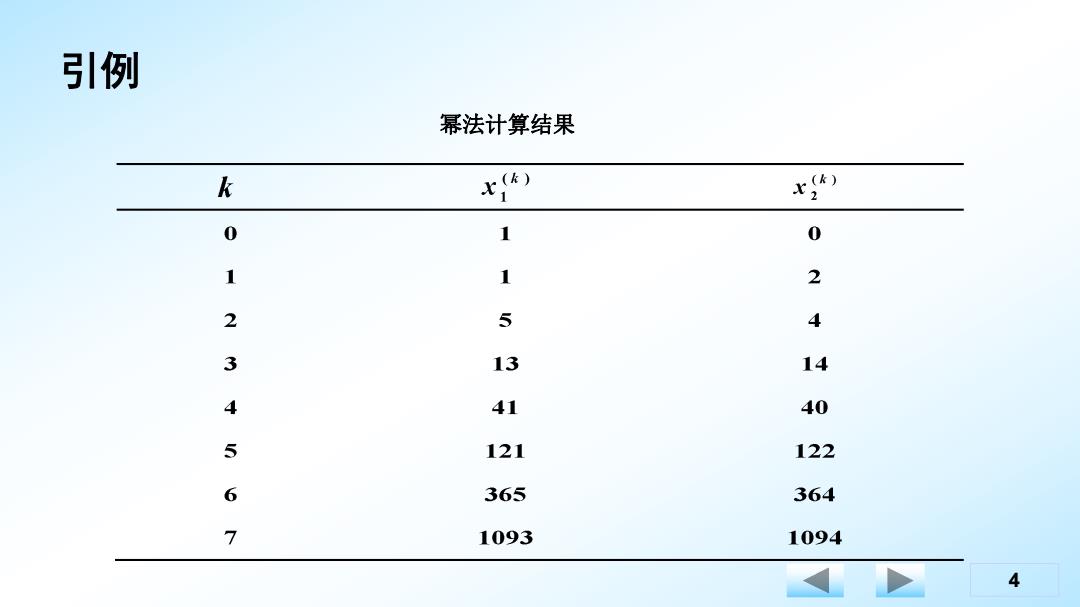
引例 幂法计算结果 k 0 1 0 1 1 2 2 5 4 3 13 14 4 41 40 5 121 122 6 365 364 7 1093 1094 4
4 引例 幂法计算结果

引例 考察两个相邻向量对应分量之比: =5 2.6 3.154 x x 2.951 3.016 2.994 x x 2 x 3.5 2.857 3.05 2.983 = 3.005 5
5 引例 考察两个相邻向量对应分量之比: (2) 1(1) 1 5 xx (3) 1(2) 1 2.6 xx (4) 1(3) 1 3.154 xx (5) 1(4) 1 2.951 xx (6) 1(5) 1 3.016 xx (7) 1(6) 1 2.994 xx (2) 2(1) 2 2 xx (3) 2(2) 2 3.5 xx (4) 2(3) 2 2.857 xx (5) 2(4) 2 3.05 xx (6) 2(5) 2 2.983 xx (7) 2(6) 2 3.005 xx