
数值微分及微分方程数值解 >数值微分显式法 >隐式方法 >Lagrange插值函数方法 >外推算法
1 Ø数值微分显式法 Ø隐式方法 ØLagrange插值函数方法 Ø外推算法 数值微分及微分方程数值解

数值微分显式法 fa+创=a+a+空a+黄a+c的) 一阶向前差商 f(a)-(a-f):O(h) h fu-创=f@-r@+gfro)gfa+oy 一阶向后差商 fa=f@)-fa-+oh) h 4 2
2 数值微分显式法 ( ) ( ) 3! ( ) 2 ( ) ( ) ( ) (3) 4 2 3 f a O h h f a h f a h f a hf a ( ) ( ) ( ) ( ) O h h f a h f a f a 一阶向前差商 ( ) ( ) 3! ( ) 2 ( ) ( ) ( ) (3) 4 2 3 f a O h h f a h f a h f a hf a ( ) ( ) ( ) ( ) O h h f a f a h f a 一阶向后差商

fa+=o+ra+艺r@+分@+ 创=a-@+分ra-蛋@+ +-fa-0=2M@+营fPa+0a的 一阶中心差商 f(a)-f(a+h)-f(a-() 2h 二阶中心差商f"a=fa+)-2f@)+a-+0) h2 3
3 ( ) ( ) ( ) ( ) ( ) 2 2 2 O h h f a h f a f a h f a 二阶中心差商 ( ) 3! ( ) 2 ( ) ( ) ( ) (3) 2 3 f a h f a h f a h f a hf a ( ) ( ) ( ) ( ) 2 2 O h h f a h f a h f a 一阶中心差商 ( ) 3! ( ) 2 ( ) ( ) ( ) (3) 2 3 f a h f a h f a h f a hf a ( ) ( ) 3 ( ) ( ) 2 ( ) (3) 5 3 f a O h h f a h f a h hf a
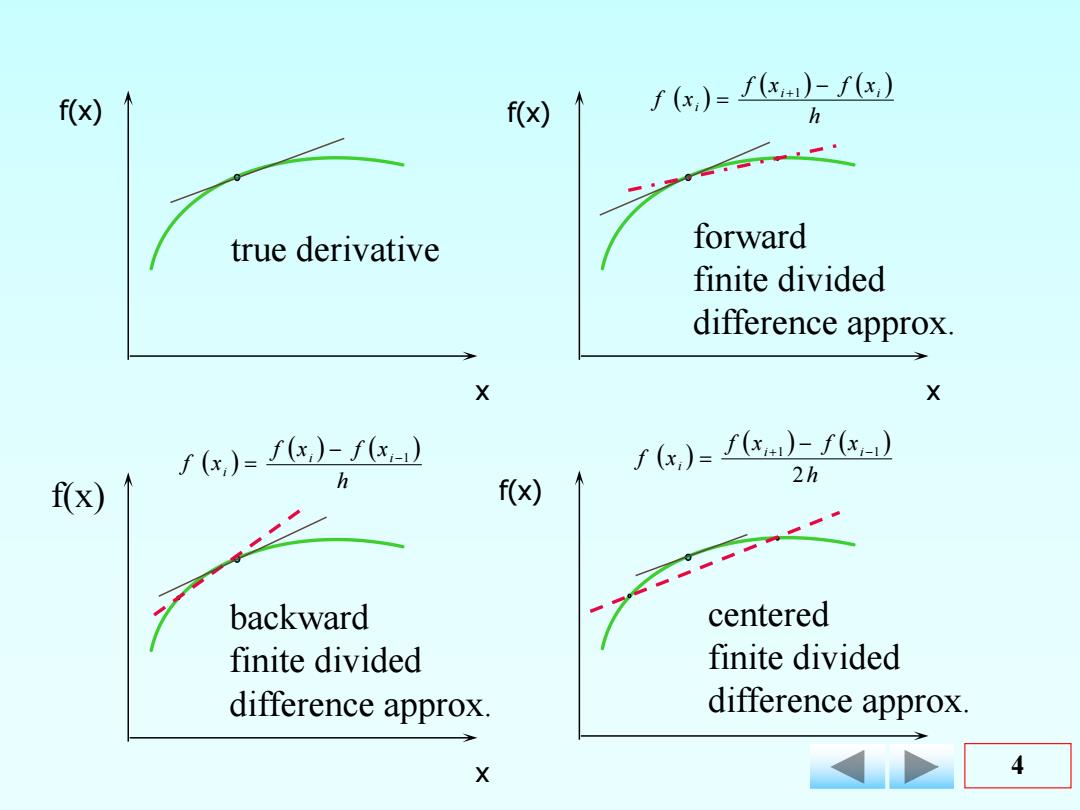
f(x) f(x) ()=()( h true derivative forward finite divided difference approx. X X f(G,)=f)-f f(x)=)-f 2h f(x) h f(x) backward centered finite divided finite divided difference approx. difference approx. X 4
f(x) x f(x) x f(x) x f(x) x true derivative forward finite divided difference approx. backward finite divided difference approx. centered finite divided difference approx. h f x f x f x i i i 1 h f x f x f x i i i 1 h f x f x f x i i i 2 1 1 4
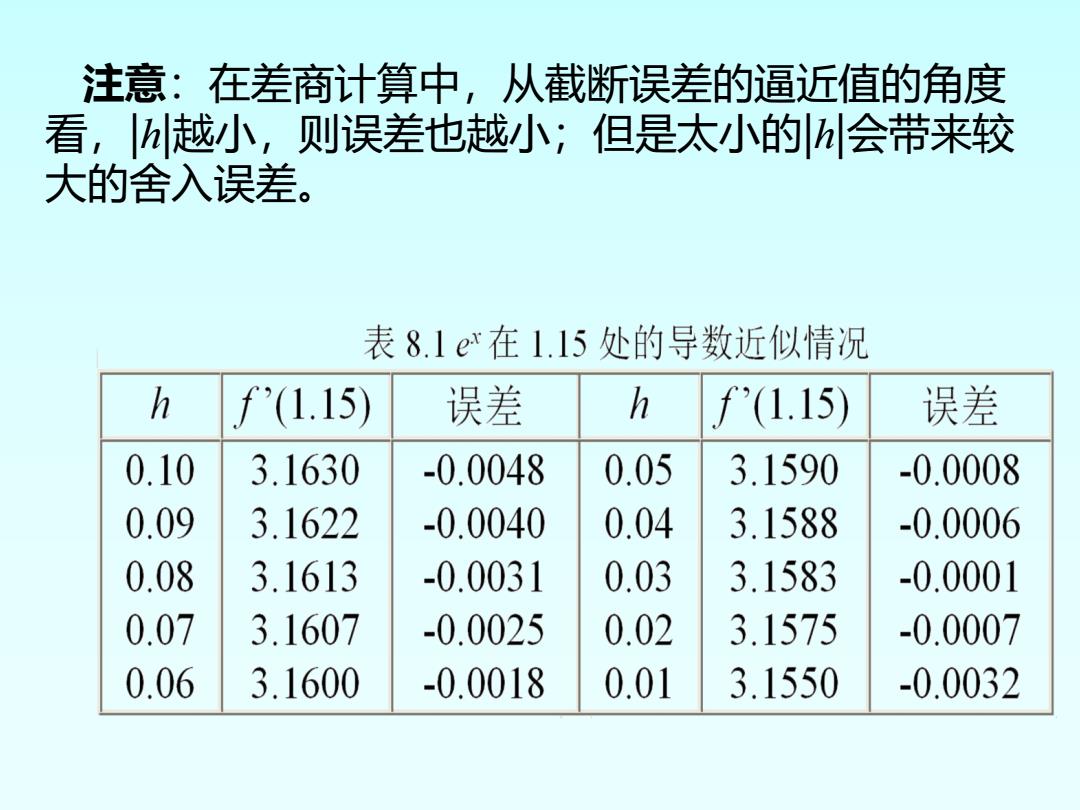
注意:在差商计算中,从截断误差的逼近值的角度 看,M越小,则误差也越小;但是太小的会带来较 大的舍入误差。 表8.1er在1.15处的导数近似情况 h f'(1.15) 误差 f'(1.15) 误差 0.10 3.1630 -0.0048 0.05 3.1590 -0.0008 0.09 3.1622 -0.0040 0.04 3.1588 -0.0006 0.08 3.1613 -0.0031 0.03 3.1583 -0.0001 0.07 3.1607 -0.0025 0.02 3.1575 -0.0007 0.06 3.1600 -0.0018 0.01 3.1550 -0.0032
注意:在差商计算中,从截断误差的逼近值的角度 看,|h|越小,则误差也越小;但是太小的|h|会带来较 大的舍入误差