
数理方程与特殊函激 第三章分离变量法(二) 主讲:杨春
第三章 分离变量法(二) 主讲:杨春

主要内容 一、拉普拉斯方程定解问题分离变量求解 二、高维混合问题分离变量求解
主要内容 一、拉普拉斯方程定解问题分离变量求解 二、高维混合问题分离变量求解
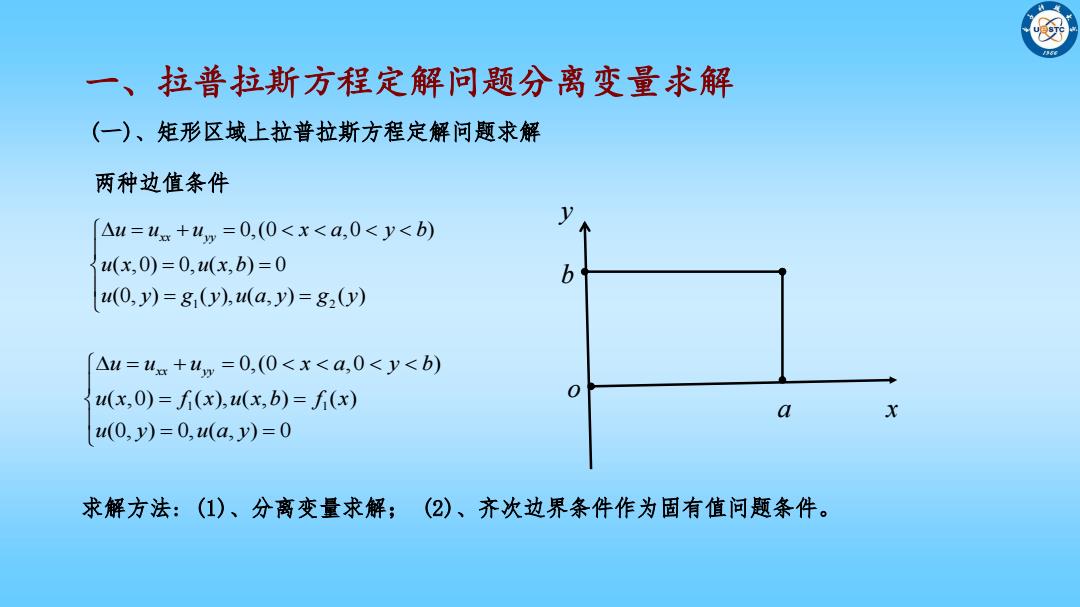
一、拉普拉斯方程定解问题分离变量求解 (一)、矩形区域上拉普拉斯方程定解问题求解 两种边值条件 △u=4.x+4p=0,(0<x<a,0<y<b) u(x,0)=0,u(x,b)=0 b u(0,y)=g(y),(a,y)=g2(y) △u=ux+4w=0,(0<x<a,0<y<b) u(x,0)=f(x),u(x,b)=f(x) 0 a X u(0,y)=0,(a,y)=0 求解方法:(1)、分离变量求解;(2)、齐次边界条件作为固有值问题条件
(一)、矩形区域上拉普拉斯方程定解问题求解 两种边值条件 一、拉普拉斯方程定解问题分离变量求解 1 2 0,(0 ,0 ) ( ,0) 0, ( , ) 0 (0, ) ( ), ( , ) ( ) u u u x a y b xx yy u x u x b u y g y u a y g y 1 1 0,(0 ,0 ) ( ,0) ( ), ( , ) ( ) (0, ) 0, ( , ) 0 u u u x a y b xx yy u x f x u x b f x u y u a y x y a b o 求解方法: (1)、分离变量求解; (2)、齐次边界条件作为固有值问题条件
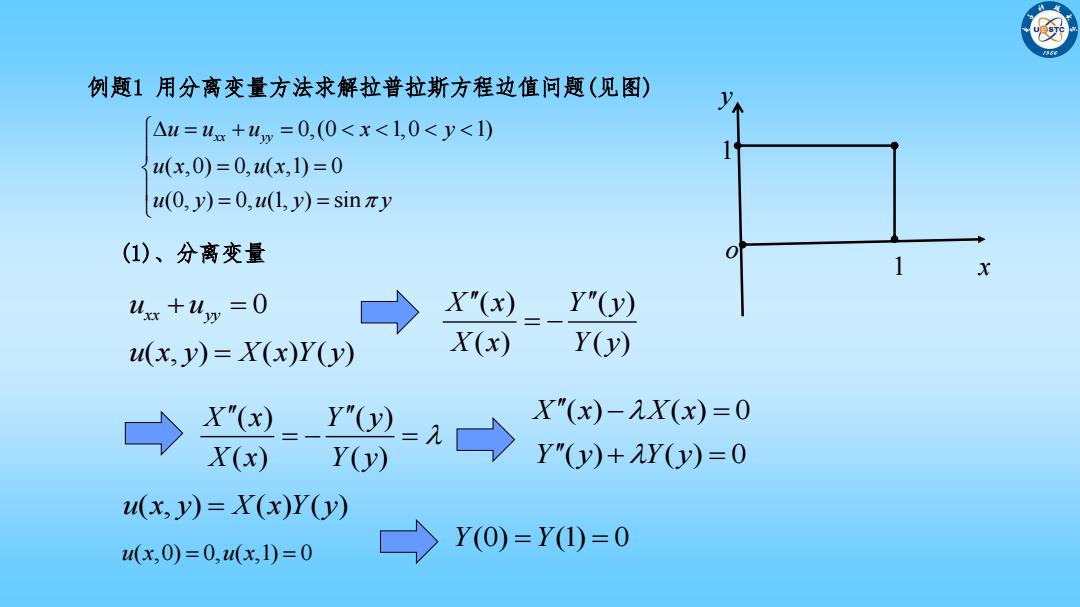
例题1用分离变量方法求解拉普拉斯方程边值问题(见图) △u=4.+4p=0,(0<x<1,0<y<1) (x,0)=0,u(x,1)=0 u(0,y)=0,u(1,y)=sin zy (1)、分离变量 X usxx +uy =0 X"(x) Y"(y) u(x,y)=X(x)Y(y) X(x) Y(y) Xx)=y"y=元> X"(x)-X(x)=0 X(x) Y(y) Y"(y)+Y(y)=0 u(x,y)=X(x)Y(y) (x,0)=0,(x,1)=0 Y(0)=Y(I)=0
例题1 用分离变量方法求解拉普拉斯方程边值问题(见图) x y 1 1 (1)、分离变量 o 0,(0 1,0 1) ( ,0) 0, ( ,1) 0 (0, ) 0, (1, ) sin u u u x y xx yy u x u x u y u y y u u xx yy 0 u x y X x Y y ( , ) ( ) ( ) ( ) ( ) ( ) ( ) X x Y y X x Y y ( ) ( ) ( ) ( ) X x Y y X x Y y X x X x ( ) ( ) 0 Y y Y y ( ) ( ) 0 u x y X x Y y ( , ) ( ) ( ) u x u x ( ,0) 0, ( ,1) 0 Y Y (0) (1) 0

Y"y)+Y(y)=0 于是得到定解问题的固有值问题 Y(0)=Y(I)=0 (2)、求解固有值问题 Y"(y)+Y(y)=0 入n=(nm)2 n=1,2,3,… Y(0)=Y(1①)=0 〉 Y(y)=sinnay (3)、求解另-个常徽分方程X"(x)-1X(x)=0· X"(x)-4X(x)=0 X,(x)=C,e"+D.e-ms X(x)=Cemx +De-nzx Y (y)=sinnay →4,(x,y)=X,x)Y,y)=(C,eax+D,)sinnzy n=1,2,3,…
(2)、求解固有值问题 2 ( ) n n n 1,2,3, ( ) ( ) 0 (0) (1) 0 Y y Y y Y Y 于是得到定解问题的固有值问题 ( ) ( ) 0 (0) (1) 0 Y y Y y Y Y Y y n y n ( ) sin (3)、求解另一个常微分方程 X x X x ( ) ( ) 0 . X x X x ( ) ( ) 0 n ( ) n x n x X x C e D e n n n ( ) n x n x X x C e D e n n n Y y n y n ( ) sin ( , ) ( ) ( ) sin n x n x u x y X x Y y C e D e n y n n n n n n 1,2,3