
极小、化方法 一、与线性方程组等价的变分问题 二、最速下降法 三、共轭梯度法(共轭斜量法) 四、预条件共轭梯度法
1 极小化方法 一、与线性方程组等价的变分问题 三、共轭梯度法(共轭斜量法) 四、预条件共轭梯度法 二、最速下降法

一、与线性方程组等价的变分问题 设x,y∈R”,记(x,y)=xTy (x,y)=(J乃,x); (t,y)=t(x,y); (x+yz)=(x,z)+(乃z); (,x)≥0,且(K,x)=0分x=0; 设A是n阶对称正定阵 (Ax,y)=(,Ay); (Ax,x)≥0,且(Ax,x)=0分x=0 2
2 设x, y∈Rn , 记 ( x , y) = x T y §( x, y ) = ( y, x ); §( tx, y ) = t ( x, y); §( x+ y, z ) = ( x, z ) + ( y, z ); §( x, x) ≥ 0, 且( x, x) = 0 x = 0; 设A是n阶对称正定阵 §( Ax, y ) = ( x, Ay ) ; §( Ax, x ) ≥0, 且( Ax, x) = 0 x = 0 一、与线性方程组等价的变分问题

设A对称正定,求解的线性方程组为 Ax=b (1) 其中A=(aj)∈Rx,x=(x1,x2,,xn),b=(b1,b2,,bn)月 对应的二次函数p:R"x”→R,称为模函数,定义为 --622宫A (2) 例:◆ A= -(x+6x+4x1x2)-(4x1+10x2) 3
3 1 2 1 2 1 ( ) , ( , , ..., ) , ( , , ..., ) n n T T ij n n A Ax b A a R x x x x b b b b 设 对称正定,求解的线性方程组为 ( ) 其中 1 1 1 ( , ) ( , ) 2 n n n n n ij i j i i i j i R R x Ax x b x a x x b x 对应的二次函数 : ,称为模函数,定义为 1 1 ( )= ( ) 2 2 2 2 1 2 1 2 1 2 4 , 1 0 ( 6 4 ) ( 4 1 0 例 ) 1 2 A = 2 6 1 ( ) = : 2 b x x x x x x x

模函数(二维) 正定 (a) (b) 负定 XTAX>0 XTAX<0 f(x) f(x) 2 2 工1 Z1 (c) (d) 正不定 不定 XTAX≥0 f(x) f(x) T2 W2 X1 4
4 模函数(二维) 正定 xT A x > 0 负定 xT A x < 0 正不定 xT A x ≥ 0 不定
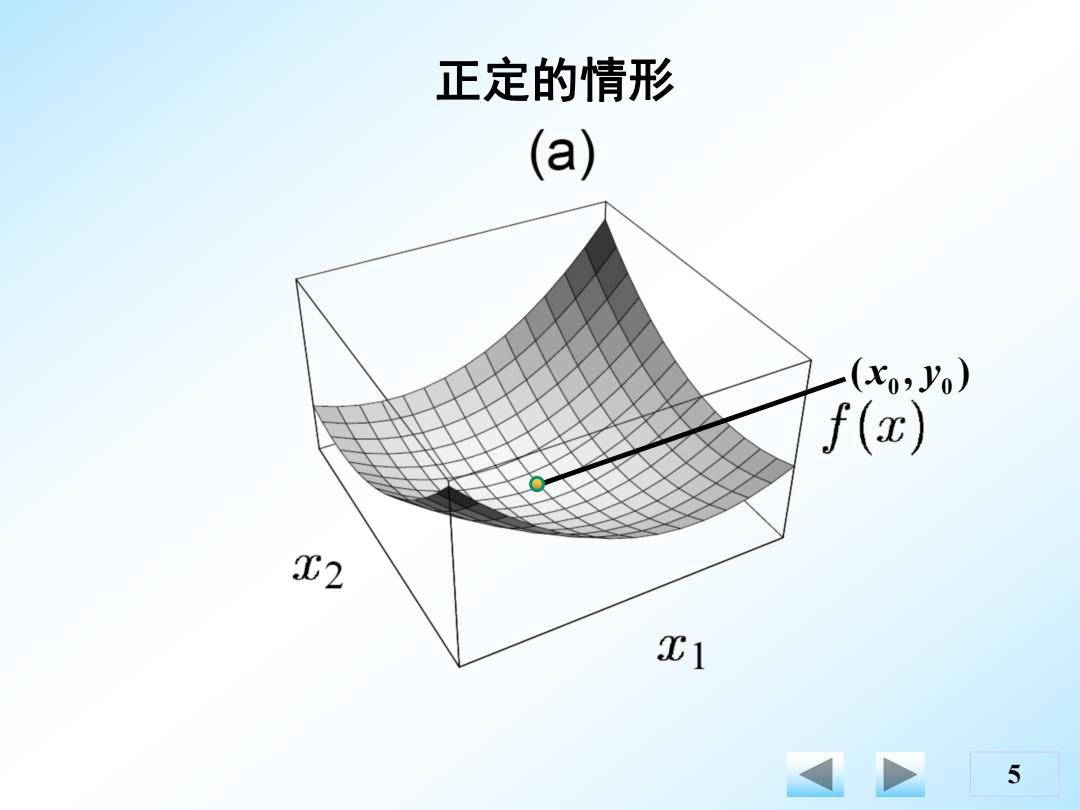
正定的情形 (a) (xo2Yo) f(x) T2 T1 5
5 ( , ) 0 0 x y 正定的情形