
牛顿迭代法 Newton迭代格式 Newton迭代法的收敛性 弦截法迭代格式 数值实验题介绍 1/23
1/23 Newton迭代格式 Newton迭代法的收敛性 弦截法迭代格式 数值实验题介绍

>牛顿(Newton)迭代法 平方根算法求√2 初值:x=1.5 迭代格式:xH1=0.5(cn+2x) (n=1,2,…) Xn Error 1.416666666666667 2.45e-003 1.414215686274510 2.12e-006 1.414213562374690 1.59e-012 1.414213562373095 2.22e-016 1.414213562373095 2.22e-016 2/23
2/23 平方根算法求 2 xn Error 1.416666666666667 2.45e-003 1.414215686274510 2.12e-006 1.414213562374690 1.59e-012 1.414213562373095 2.22e-016 1.414213562373095 2.22e-016 Ø牛顿(Newton)迭代法

基本思想: 将方程x)=0中函数fx)线性化,以线性方程的解逼近非线性 方程的解. 设函数fx)在有根区间[a,b]二次连续可微,则x)在x处的泰 勒展开式为: fx)=)+f'xx-x)+52(x-x,} 2 只取关于x线性项,有 f(xo)+f'(x)(x-x)=0 设f'(x,)≠0,其解记为 f(xo) x=x0- (*) f'(x,) 3/23
3/23 将方程 f(x)=0中函数 f(x)线性化,以线性方程的解逼近非线性 方程的解. 设函数 f(x)在有根区间[a,b]二次连续可微,则 f(x)在x0处的泰 勒展开式为: 2 0 0 0 0 ( ) 2! "( ) ( ) ( ) '( )( ) x x f f x f x f x x x ( ) '( )( ) 0 f x0 f x0 x x0 只取关于x线性项,有 设 f '(x0 ) 0 ,其解记为 '( ) ( ) 0 0 0 f x f x x x (*)
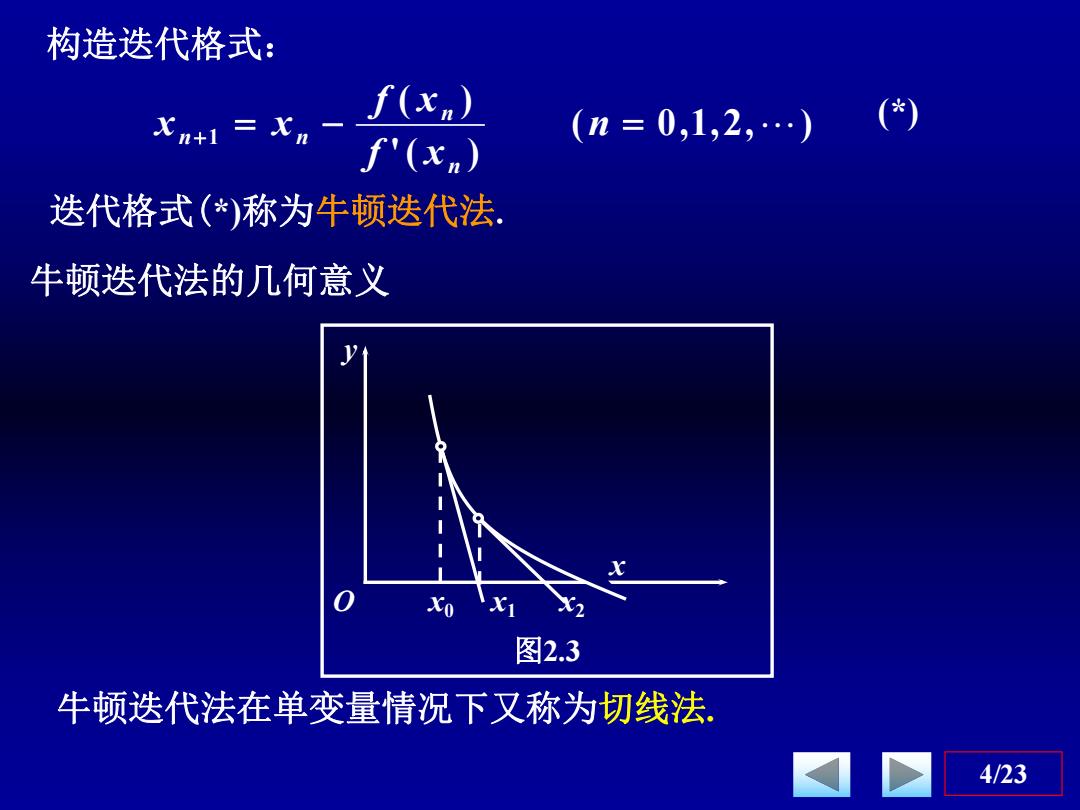
构造迭代格式: f(xn) Xn+1=Xm (n=0,1,2,…) (*) f'(x) 迭代格式(*)称为牛顿迭代法. 牛顿迭代法的几何意义 Xo 图2.3 牛顿迭代法在单变量情况下又称为切线法 4/23
4/23 牛顿迭代法的几何意义 y x O x0 x1 x2 图2.3 牛顿迭代法在单变量情况下又称为切线法. ( 0,1,2, ) '( ) ( ) 1 n f x f x x x n n n n (*) 迭代格式(*)称为牛顿迭代法. 构造迭代格式:

应用一求正数平方根算法 设C>0,x=√C x2 - C=0 令fx)=x2-C,则 f'(x)=2x x2-C Xn+l 三 2Xn 尤n+1= 2 5/23
5/23 设C > 0, x C x2 – C = 0 令 f(x) = x2 – C , 则 f (x) 2x n n n n x x C x x 2 2 1 [ ] 2 1 1 n n n x C x x 应用——求正数平方根算法