方法1.投影法(“先一后二”) 如图:闭区域2在x0y z=2(比,y) 面上的投影为闭区域D, S1:z=z1(x,y), S2:7=72(X,y) =(比,y) 过点(x,y)∈D作直线, 从名穿入,从3穿出. =y(x =y(x)
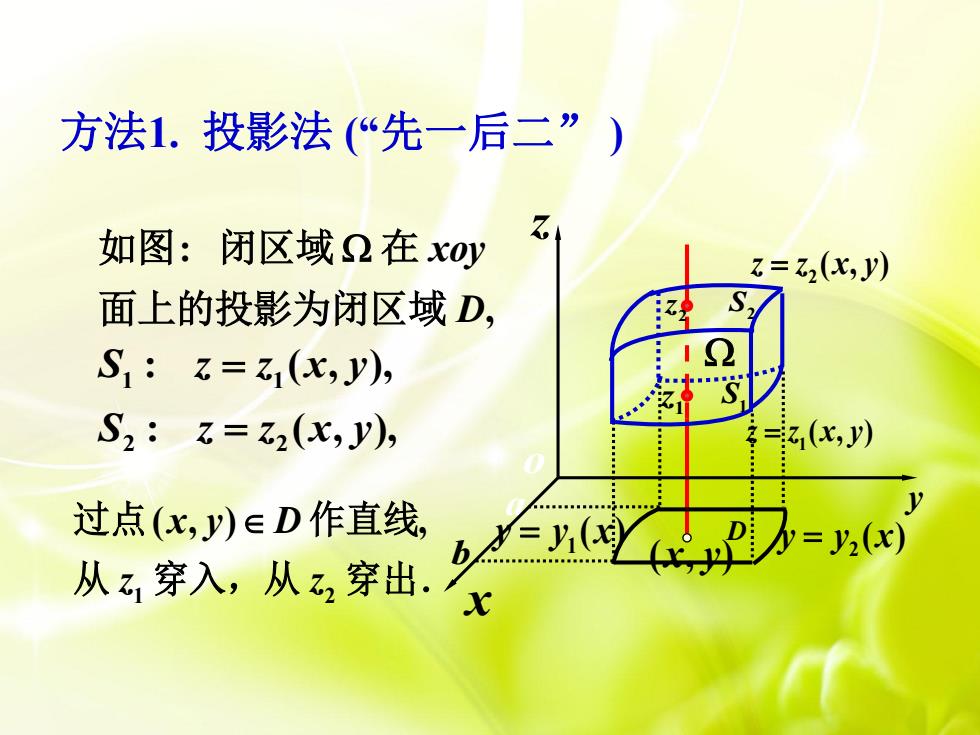
: , xoy D 如图 闭区域 在 面上的投影为闭区域 1 1 2 2 : ( , ), : ( , ), S z z x y S z z x y 1 2 ( , ) , x y D z z 过点 作直线 从 穿入,从 穿出. 1 z 2 z S2 S1 1 z z x y ( , ) 2 z z x y ( , ) a b 1 y y x ( ) 2 y y x ( ) ( , ) x y x y z o D 方法1. 投影法 (“先一后二” )

在此情形下积分区域Ω可表示为 2:{(x,y,z)川z1(x,y)≤z≤z2(x,y),(x,y)∈D} 先将x,y看作定值,将f(x,y,z)只看作z的函 数,则在区间[z(x,y),2(x,y)门上对在积分得 F=f地 计算F(K,y)在闭区间D上的二重积分 顶fav-Fxo=fc2wo
1 2 , ( , , ) ( , ), ( , ) x y f x y z z z x y z x y 先将 看作定值,将 只看作 的函 数,则在区间[ ]上对在积分得 2 1 ( , ) ( , ) ( , ) ( , , ) z x y z x y F x y f x y z dz 计算 F x y D ( , ) 在闭区间 上的二重积分 1 2 :{( , , ) | ( , ) ( , ),( , ) } x y z z x y z z x y x y D 在此情形下积分区域 可表示为 2 1 ( , ) ( , ) ( , ) [ ( , , ) ] . z x y z x y D D F x y d f x y z dz d

假设D:y,(x)≤y≤y,(x),u≤x≤b, j∬fx,八z) = 32(x,y) f(x,y,z). 三次积分 注意 这是平行于z轴且穿过闭区域Ω内部的直线 与闭区域Ω的边界曲面S相交不多于两点情形
f x y z dv ( , , ) 注意 z S 这是平行于 轴 且 穿 过 闭 区 域 内 部 的 直线 与 闭 区 域 的 边界 曲 面 相 交不 多 于两 点情形. 1 2 假设 D y x y y x a x b : ( ) ( ), , 得 2 2 1 1 ( ) ( , ) ( ) ( , ) ( , , ) . b y x z x y a y x z x y dx dy f x y z dz 三次积分
例1计算三重积分∬xdxdydz,其中2为三个 坐标面及平面x+2y+z=1所围成的闭区域。 解:设2在xoy面上的投影为D,则 D:{x,y川0≤y≤(1-x),0≤x≤1 又有0≤z≤1-x-2y C0,0,1) 0≤z≤1-x-2y B(0, 即2:0≤y≤1-) 0≤x≤1 A(1,0,0)
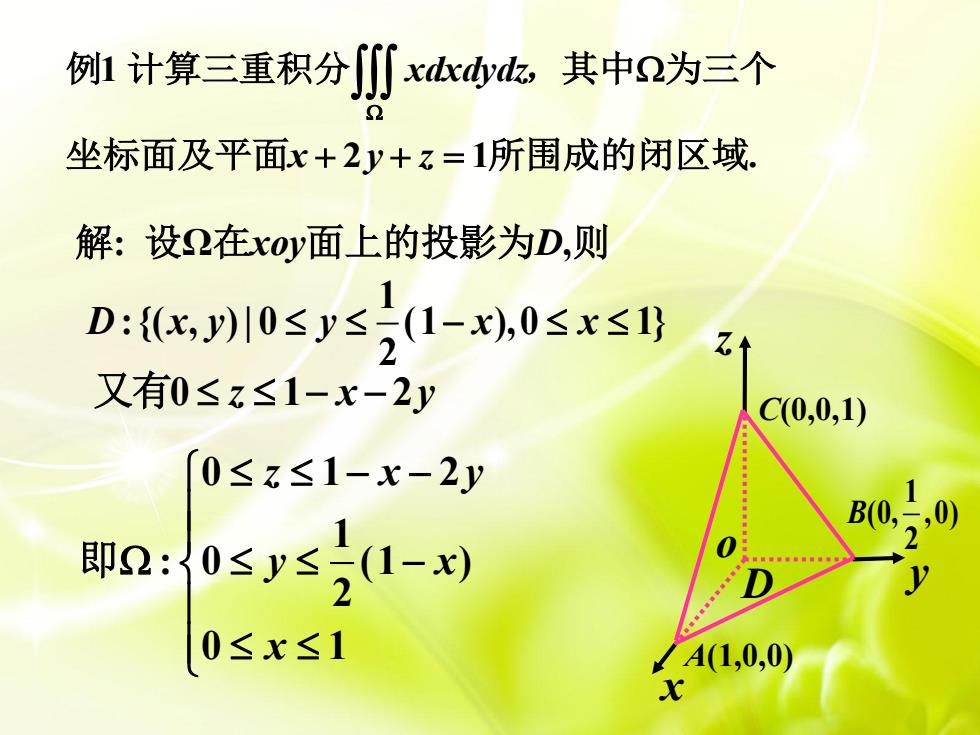
1 2 1 . xdxdydz x y z 例 计算三重积分 ,其中 为三个 坐标面及平面 所围成的闭区域 解: 0 1 2 1 : 0 (1 ) 2 0 1 z x y y x x 即 1 :{( , ) | 0 (1 ),0 1} 2 D x y y x x 又有0 1 2 z x y 设Ω在xoy面上的投影为D,则 D x y z o A(1,0,0) C(0,0,1) 1 (0, ,0) 2 B
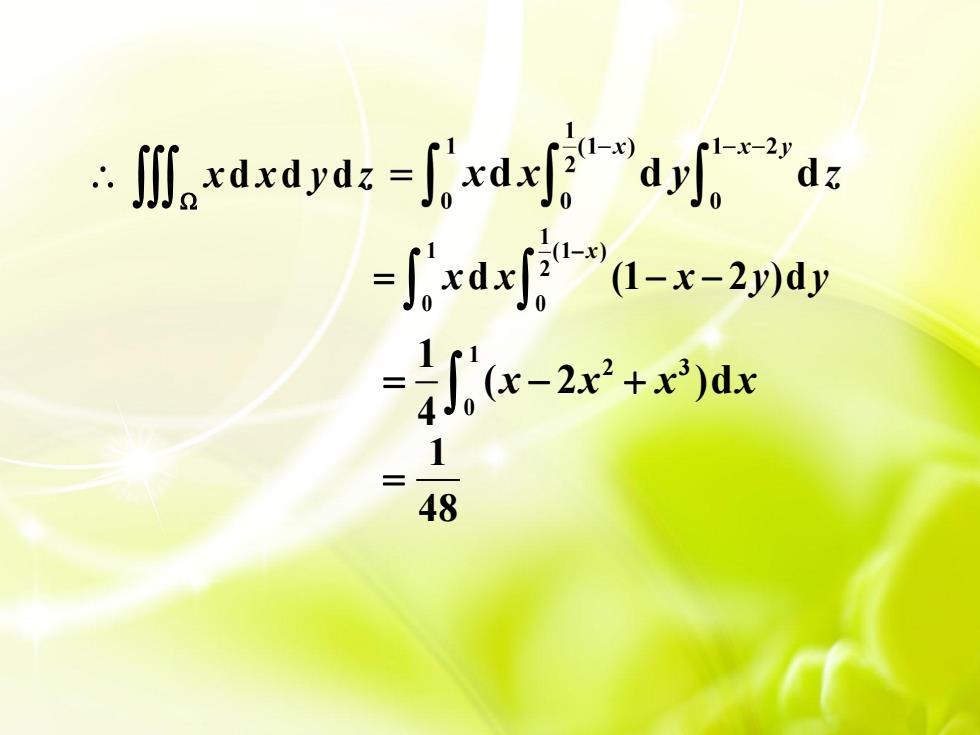
。xdxdyd:-jxa时官0ar”a: -,xdxj"A-x-2y)ay =∫x-2.x2+x)dx 1 48
x x y z d d d 1 1 (1 ) 2 0 0 d (1 2 )d x x x x y y 1 2 3 0 1 ( 2 )d 4 x x x x 1 48