
第三节平面及其方程 ·一、曲面方程和曲线方程的橇念 ·二、平面的点法式方程 ·三、车面的一般方程 ·四、两平面的夹角 。五、小结
第三节 平面及其方程 • 一、曲面方程和曲线方程的概念 • 二、平面的点法式方程 • 三、平面的一般方程 • 四、两平面的夹角 • 五、小结

一、曲面方程与曲线方程的概念 曲面的实例:水桶的表面、台灯的罩子面等. 曲面在空间解析几何中被看成是点的几何轨迹. 曲面方程的定义: 如果曲面S与三元方程F(x,y,z)=0有下述关系: (1)曲面S上任一点的坐标都满足方程; (2)不在曲面S上的点的坐标都不满足方程; 那么,方程F(x,y,z)=0就叫做曲面S 的方程,而曲面S就叫做方程的图形
水桶的表面、台灯的罩子面等. 曲面在空间解析几何中被看成是点的几何轨迹. 曲面方程的定义: 如果曲面S 与三元方程F( x, y,z) 0有下述关系: (1) 曲 面S上任一点的坐标都满足方程; (2)不在曲面S上的点的坐标都不满足方程; 那么,方程F( x, y,z) 0就叫做曲面S 的方程,而曲面S就叫做方程的图形. 曲面的实例: 一、曲面方程与曲线方程的概念
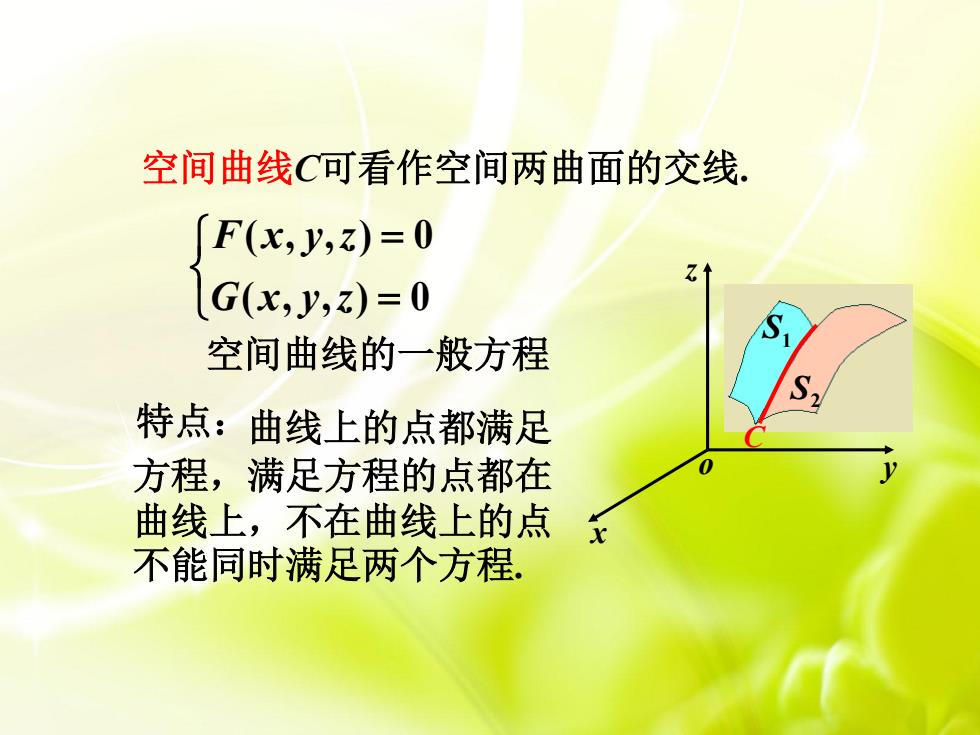
空间曲线C可看作空间两曲面的交线, F(x,y,z)=0 G(x,y,z)=0 空间曲线的一般方程 特点:曲线上的点都满足 方程,满足方程的点都在 曲线上,不在曲线上的点 不能同时满足两个方程
( , , ) 0 ( , , ) 0 G x y z F x y z 空间曲线的一般方程 曲线上的点都满足 方程,满足方程的点都在 曲线上,不在曲线上的点 不能同时满足两个方程. x o z y S1 S2 C 空间曲线C可看作空间两曲面的交线. 特点:

二、平面的点法式方程 如果一非零向量垂直 于一平面,这向量就叫做 该平面的法线向量. 法线向量的特征:垂直于平面内的任一向量 已知i={A,B,C},M(xo,y,), 设平面上的任一点为M(x,y,z) 必有MnM⊥i→M,M,n=0
x y z o M0 M 如果一非零向量垂直 于一平面,这向量就叫做 该平面的法线向量. 法线向量的特征:垂直于平面内的任一向量. 已知 n { A, B, C } , ( , , ), 0 0 0 0 M x y z 设平面上的任一点为 M ( x , y , z) M M n 必有 0 0 M 0M n 二、平面的点法式方程 n

MoM={x-xo,y-yo,-Zo} .A(x-x)+B(y-y0)+C(z-z0)=0 平面的点法式方程 其中法向量i={A,B,C},已知点(xo,y,) 平面上的点都满足上方程,不在平面上的点 都不满足上方程,上方程称为平面的方程,平 面称为方程的图形
{ , , } 0 0 0 0 M M x x y y z z ( ) ( ) ( ) 0 A x x0 B y y 0 C z z 0 平面的点法式方程 平面上的点都满足上方程,不在平面上的点 都不满足上方程,上方程称为平面的方程,平 面称为方程的图形. 其中法向量 n { A, B,C } , 已知点 ( , , ). 0 0 0 x y z