
第二节复数的三角表示 2.1复数的模和辐角 2.2复数模的三角不等式 2.3复数的三角表示 2.4用复数的三角表示作乘除法 2.5复数的乘方与开方
第二节 复数的三角表示 2.1 复数的模和辐角 2.2 复数模的三角不等式 2.3 复数的三角表示 2.4 用复数的三角表示作乘除法 2.5 复数的乘方与开方

2.1复数的模(或绝对值)和辐角 1.如果是一个不等于零的复数,把它对应的 向量的长度叫做z的模,记做z 2=r=Vx2+2. 显然下列各式成立 Pz=x+iy x≤z, y≤z, z≤x+y,zz=z2=zl
2.1 复数的模(或绝对值)和辐角 . 2 2 z r x y x y x y o z x iy P 显然下列各式成立 r x z, y z, z x y , . 2 2 zz z z 向量的长度叫做z的模 ,记做 z 1.如果z是一个不等 于零的复数,把它对应 的 2

2.复数z≠0,把它对应的向量的方向角称为z 的辐角. z的辐角记做:Argz 说明 任何一个复数z≠0有无穷多个辐角, 如果0,是其中一个辐角,那么z的全部辐角为 Argz=0,+2km(k为任意整数). 特殊地,当z=0时,z=0,辐角不确定
说明 任何一个复数 z 0有无穷多个辐角, , 如果 1 是其中一个辐角 Arg 2 π ( ). z 1 k k为任意整数 特殊地, 当 z 0时, z 0, 那么 z的全部辐角为 辐角不确定. 的辐角. 2.复数z 0,把它对应的向量的方向 角称为z z的辐角记做 : A rgz 3

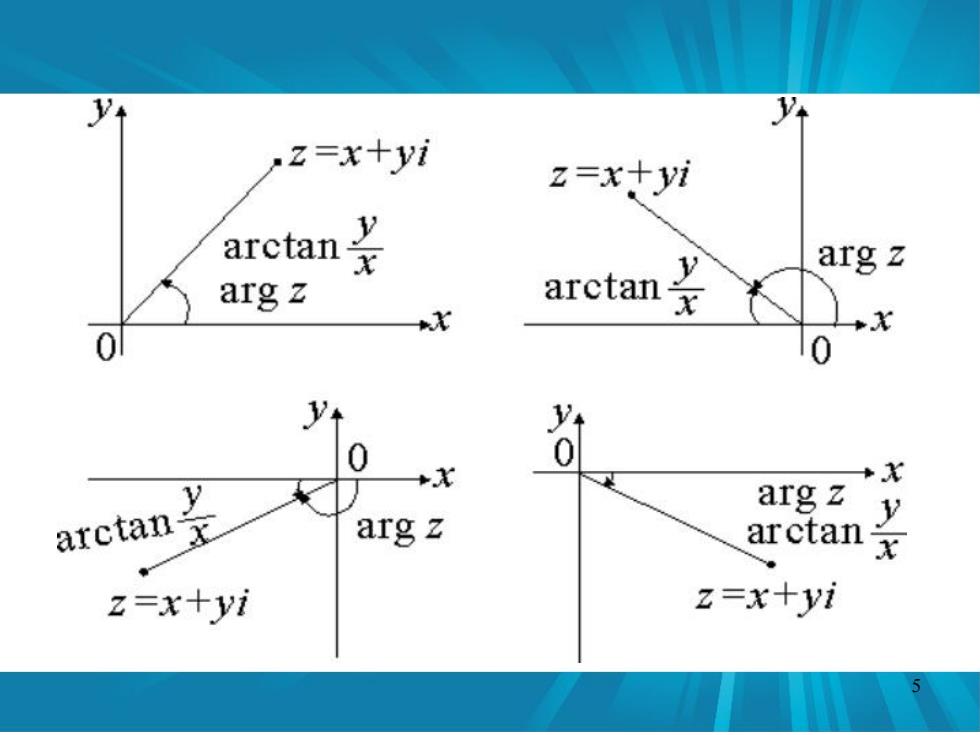
3辐角主值的定义: 在z(≠0)的辐角中把满足-元<0。≤π的0。 称为Arg的主值,记作O,=argz. z≠0辐角的主值 arctan-, x>0, X 元 士 x=0,y≠0, argz=了 arctan±元, x<0,y≠0, X 元, x<0,y=0. (其中-<arctan'< 2
3.辐角主值的定义: Arg , arg . ( 0) , π π 0 0 0 z z z 称为 的主值 记作 在 的辐角中把满足 的 x 0, ) 2 arctan 2 ( x y 其中 z 0 辐角的主值 arg z x 0, y 0, x 0, y 0, x 0, y 0. arctan , x y , 2 π arctan π , x y π , 4
12 Z=x+yi z=x十yi aretan关 arg z arctan若 arg Z X 0 0 +X +X arctan arg z y arg z arctan x z=x+yi z=x+yi
5