
第四节无穷大与复球面 一、无穷远点 二、复球面
第四节无穷大与复球面 二、复球面 一、无穷远点

一、 无穷远点 1.无穷大定义 1 0∞= 0 2.和有限数的四则运算 a士o0=0士a=o(a≠0) a·0=0·a=o(a≠0) 吕-(a*0,g-0a≠”-nla≠o)
( 0), 0 a = a = 0( ), a a = ( ) a a a = a = (a 0) a = a = (a ) 0 1 = 一、无穷远点 1.无穷大定义 2.和有限数的四则运算

说明: ()但是下列运算无意义 o士o060,8 (2)对于复数0,其模规定为+∞,而实部、虚部和 辐角均没有意义 (3)在复变量情况下,∞是没有符号的.与实变量情 况不一样,±o是有区别的. (4)对于∞,可设想在复平面上有一理想点与它对 应,此点称为无穷远点
0 0 ,0 , , 应,此点称为无穷远点. (4)对于,可设想在复平面上有一理想点与它对 说明: (1)但是下列运算无意义 辐角均没有意义 (2)对于复数,其模规定为+ ,而实部、虚部和 , . (3) , 况不一样 是有区别的 在复变量情况下 是没有符号的.与实变量情

(⑤)复平面加上无穷远点称为扩充复平面 (⑥)扩充复平面上的每一条直线都通过无穷远点. (7)无穷远点的邻域:是包括无穷原点在内的圆周 z=M的外部. >M (8)无穷远点的空心邻域:M<z<+o 二、复球面
的外部. (7)无穷远点的邻域:是包括无穷原点在内的圆周 z = M (8)无穷远点的空心邻域:M z +. z M (6)扩充复平面上的每一条直线都通过无穷远点. (5)复平面加上无穷远点称为扩充复平面. 二、复球面
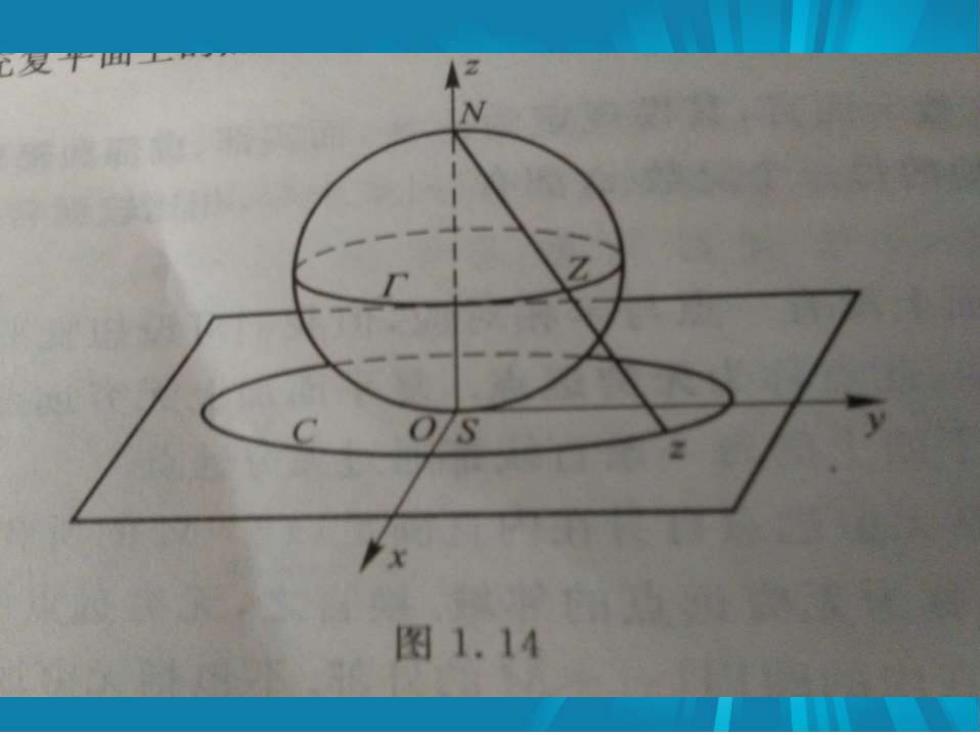
图1.14