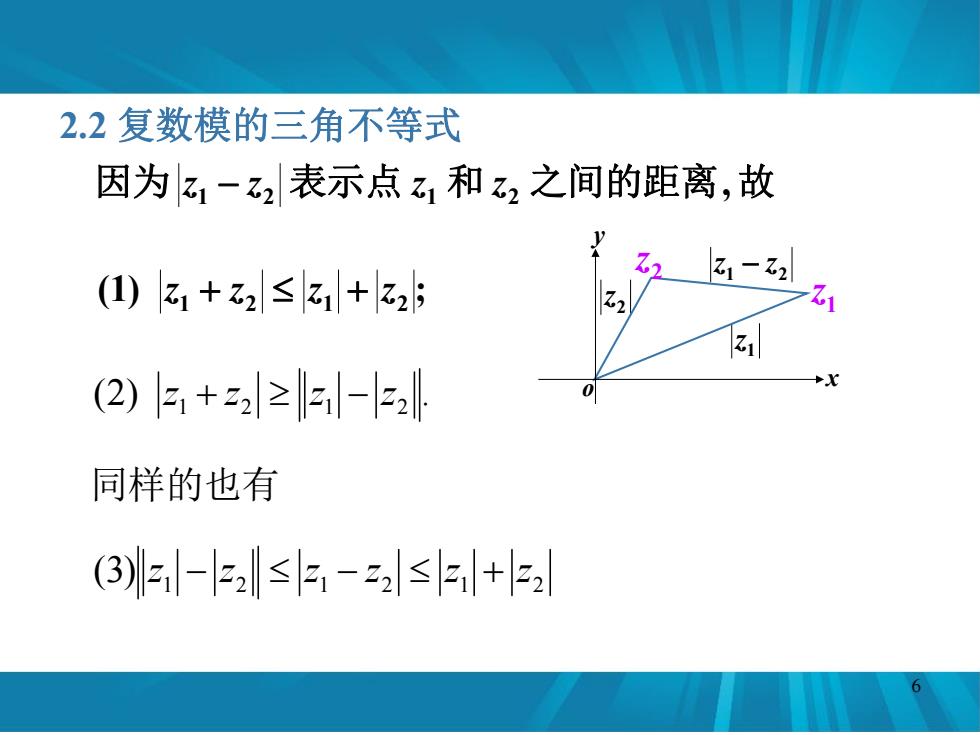
2.2复数模的三角不等式 因为乙1-乙2表示点1和2之间的距离,故 1-2 (1)31+z2≤z1+z25 31 (2)3+2≥-2 同样的也有 (3)-32≤3,-22≤+2
2.2 复数模的三角不等式 (1) ; 1 2 1 2 z z z z (2) . 1 2 1 2 z z z z , 因为 z1 z2 表示点 z1 和 z2 之间的距离 故 1z 2 z 1 2 z z x y o 1z 2 z 6 同样的也有 1 2 1 2 1 2 (3) z z z z z z

2.3复数的三角表示和指数表示 对于一个不等于0的复数z=x+y,它的实部与虚部 同它的模和辐角之间的关系为 x=rcose,y=rsine 复数可以表示成z=r(cos0+isin) 复数的三角表示式 再利用欧拉公式e0=cos0+isin6, 复数可以表示成z=rei0 复数的指数表示式
x rcos, y rsin 复数可以表示成 z r(cos isin ) 复数的三角表示式 再利用欧拉公式 cos sin , e i i 复数可以表示成 i z re 复数的指数表示式 2.3 复数的三角表示和指数表示 7 同它的模和辐角之间的关系为 对于一个不等于0的复数z x iy,它的实部与虚部

说明: 1由于复数的辐角有无穷多,所以复数的三角表示 式不唯一 即 i(co8+isin吧)=(cos,识+isine,) 则可推出 1=2,091=02+2kπ 2.表达式中的r,分别是z的模和辐角或者辐角主值 并且符合表达式的形式
即 (cos sin ) (cos sin ) 1 1 1 2 2 2 r i r i 则可推出 r1 r2 ,1 2 2k 8 . 2. , , 并且符合表达式的形式 表达式中的r 分别是z的模和辐角或者辐角主值 . 1. , 式不唯一 由于复数的辐角有无穷多 所以复数的三角表示 说明:

例1将下列复数化为三角表示式与指数表示式: (1)z=-V12-2i; (②z=sin爱+ioo号 解 (I)r=z=√2+4=4,因为z在第三象限, 所以9=arca(-)=atm /3 故三角表示式为 =-in-刘小
例1 将下列复数化为三角表示式与指数表示式: ; 5 cos 5 (1) 12 2 ; (2) sin z i z i 解 (1) r z 12 4 4, 因为 z 在第三象限, π 12 2 arctan 所以 3 3 arctan 故三角表示式为 , 6 5 sin 6 5 4 cos z i 9

指数表示式为 5 2=4e (2)z=sin +icos 5 5 显然r=z=1, 元 3元 sin=cos cos 5 10 =sin 3π 25) =sin 10 故三角表示式为 3 3元 +isin 10 10 3 指数表示式为 i z=el0' 10
指数表示式为 4 . 65 i z e 5 cos 5 (2) sin z i 显然 r z 1, 2 5 cos 5 sin , 103 cos 2 5 sin 5 cos , 103 sin 故三角表示式为 , 103 sin 103 cos z i 指数表示式为 . 103 i z e 10