《复变函数与积分变换》课程教学课件（PPT讲稿）第三章 复变函数的积分 3.1 复积分概述

第一节复变函数积分 一、复积分的定义 二、复积分的性质 三、复积分的计算

第一节复变函数积分 一、复积分的定义 二、复积分的性质 三、复积分的计算

1.关于曲线方向的说明： 一般：曲线C的正方向总是指从起，点到终点 的方向，那么终点到起点的方向就是曲线C的 负向，记为C 2.闭曲线正向的定义： C-一闭曲线正方向观察者顺此方向沿前进 一周的内部一直在观察者的左边。与之相 反的方向就是曲线的负方向

一般: 曲线C的正方向总是指从起点到终点 的方向.那么终点到起点的方向就是曲线C的 负向,记为C- C−−闭曲线正方向观察者顺此方向沿前进 一周的内部一直在观察者的左边。与之相 反的方向就是曲线的负方向. 2.闭曲线正向的定义: 1.关于曲线方向的说明： 2

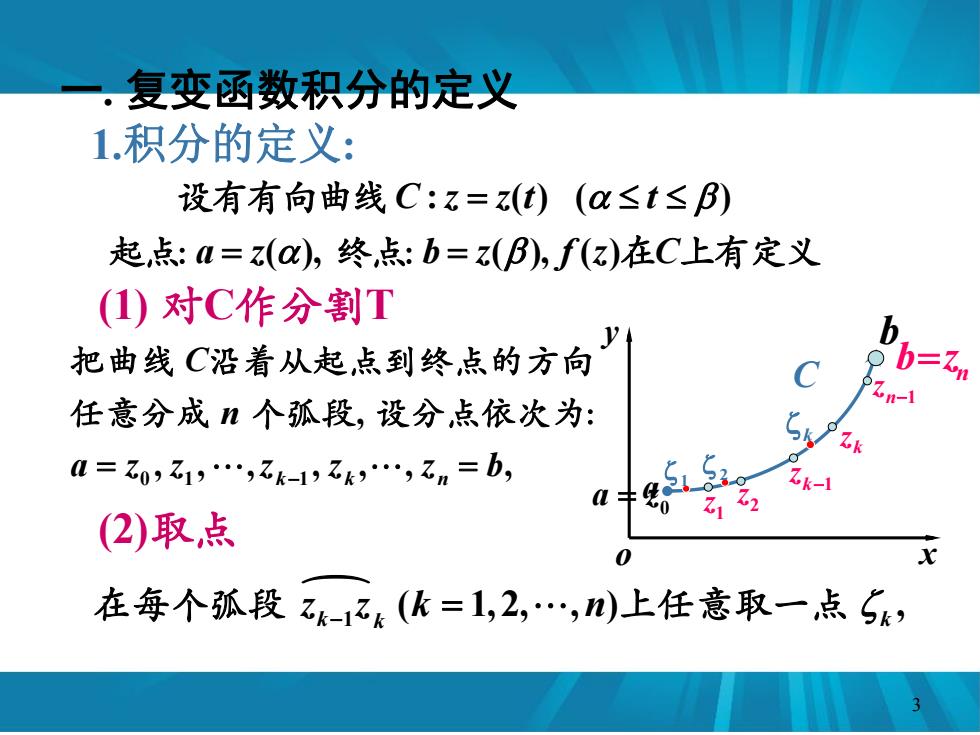
.复变函数积分的定义 1.积分的定义： 设有有向曲线C:z=z(t)(a≤t≤B) 起点：M=z(),终，点：b=z(B),f(z)在C上有定义 (1)对C作分割T 把曲线C沿着从起点到终点的方向 任意分成n个孤段，设分，点依次为： 0=乙0，乙1，.，乙k-1,乙k,.,乙n=b, 3k1 (2)取，点 00312 0 在每个孤段乙k-1不k(k=1,2,.,)上任意取一点Sk

1.积分的定义: : ( ) ( ) ( ), ( ), ( ) C z z t t a z b z f z C          设有有向曲线 起点: 终点: 在 上有定义 o x y a b n1 z k z k1 z 2 z 1z k  C 1  2   1 ( 1, 2, , ) , k k k z z k n  在每个弧段    上任意取一点 一. 复变函数积分的定义 0 1 1 , , , , , , , , k k n C n a z z z z z b      把曲线 沿着从起点到终点的方向 任意分成 个弧段 设分点依次为: (1) 对C作分割T (2)取点 0 a  z n bz 3

③)作(Rinmann)和 S.=官f6,&,-)=25.aw 这里△k=乙k-乙k-1,△Sk=乙k-2的长度， 记6(=TD=max{As}, l≤k≤n (4)求极限 当n无限增加且6→0时， 91 k-1 如果不论对C的分法及Sk的 0 X 取法如何，Sn有唯一有限的极限J,则称f(z)沿着C的正 向可积，极限值J称为函数∫(z)沿曲线C的积分，记为 Jf(z)dz

1 1 1 ( ) ( ) ( ) , n n n k k k k k k k S f  z z f  z           o x y A B n1 z k z k1 z 2 z 1z k  C 1  2  1 ( ) max{ }, k k n  T s   记    , , 这里 zk  zk  zk1 sk  zk1zk的长度 ( 当n无限增加且   0时, , ( ) ( ) , , C k n J f z S J C f z C 如  极限值 称为函数 果不论对 的分法及 的 取法如何 有 有 沿曲线 唯一 限的极限 则称 沿 的积分 着 的 向可积, 记为 正 (3)作(Rinmann)和 (4)求极限 ( )d C f z z  4

复变函数 即：厂cfa)k=im∑f5)△z: 8→0 k=1 关于定义的说明： ()用。f(z)dz表示f(2)沿着曲线C的负向的积分 (2)f(z)沿着此闭曲线C的积分也可以记为∮f(z)k。 (3)如果C是x轴上的区间a≤x≤b,而f(z)=(x), 这个积分定义就是一元实变函数积分的定义 一般不能把∫f(a)dz写成∫”f(z)dk形式 (4) 因为：一般f(z)z的值不仅与起点，终点b有关， 更与积分路线C有关

关于定义的说明: (3) , ( ) ( ), . 如果 C 是 x 轴上的区间a  x  b 而 f z  u x 这个积分定义就是一元实变函数积分的定义 0 1 : ( ) lim ( ) . n n k k C k f z dz f z         即  (1) ( )d ( ) C f z z f z 用  表示 沿着曲线C的负向的积分 (4) ( )d ( ) b C a f z z f z dz 一般不能把 写成 形式 ( , C )d C f z z a b 因为  :一般 的值不仅与起 更与积分路 点 终点 有关， 线 有关 (2) f (z) C f (z)dz. C 沿着此闭曲线 的积分也可以记为 5