《复变函数与积分变换》课程教学课件（PPT讲稿）第四章 解析函数的级数表示 4.3 解析函数的泰勒展开

第三节泰勒级数 一、泰勒定理 二、将函数展成泰勒级数 三、典型例题 四、小结与思考

第三节泰勒级数 一、泰勒定理 二、将函数展成泰勒级数 三、典型例题 四、小结与思考

一、泰勒定理 1.定理4.6设函数f(z)在区域D内解析，z为D内一个点， R为z到D的边界的最短距离，则当z-<R时，f(z)可 展成幂级数，即 f)-Eo(-zr.-eK n=0 其中c,=(》.并且展开式是唯一的 n 则称它为f(z)在z的泰勒展开式，右端的级数为f(z) 在z点的泰勒级数

2 一、泰勒定理 展成幂级数 即 为 到 的边界的最短距离 则当 时 可 定理 设函数 在区域 内解析 为 内一个点 , , , ( ) 1. 4.6 ( ) , , 0 0 0 R z D z z R f z f z D z D −  f z c z z z K n n =  n −   = ( ) ( ) , 0 0 , . ! ( )0 ( ) 其中 并且展开式是唯一的 n f z c n n = . ( ) , ( ) 0 0 在 点的泰勒级数 则称它为 在 的泰勒展开式 右端的级数为 z f z z f z

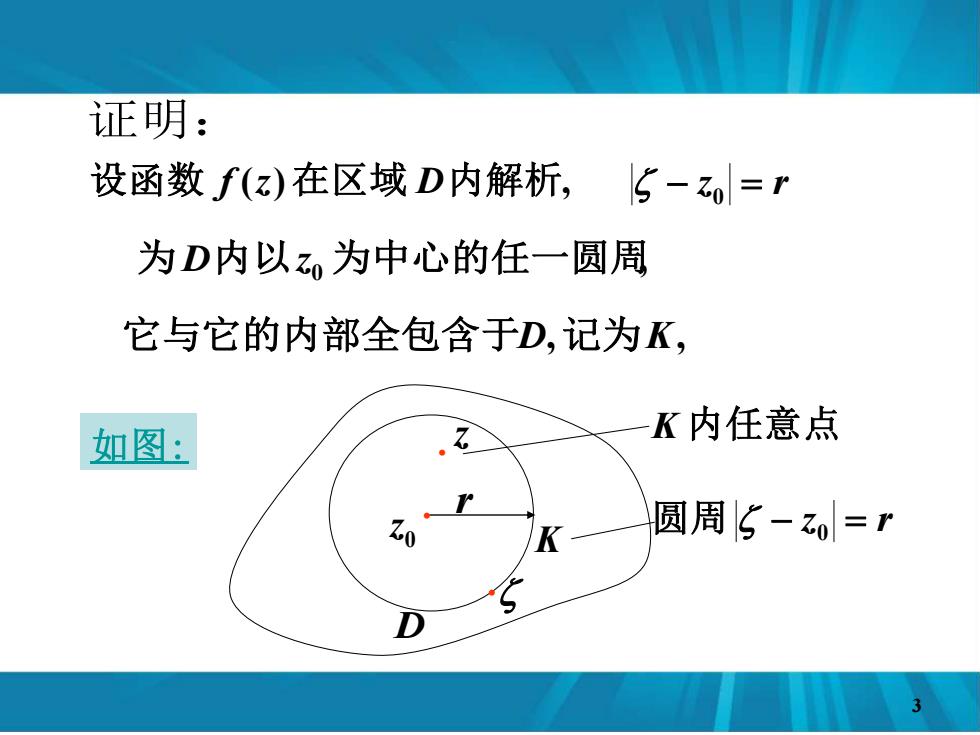
证明： 设函数f(z)在区域D内解析，5-z=r 为D内以z为中心的任一圆周 它与它的内部全包含于D,记为K, 如图： K内任意点 Zo K 圆周5-z0=1

D z K . 内任意点 设函数 f (z)在区域 D内解析, , 为D内以z0 为中心的任一圆周 如图 : r 0 z . K − z = r 圆周  0 .  0  − z = r 它与它的内部全包含于D,记为 K, 3 证明：

由柯西积分公式，有 f(z)= 1f2a5,其中K取正方向. 2niks-z 因为积分变量6取在圆周K上，点z在K的内部， 所以 Z-Zo <1. 5-z0 1 1 则 5-z5-01-z-0 5-z0

由柯西积分公式 , 有  − = K z f i f z d , ( ) 2π 1 ( )    其中 K 取正方向. 因为积分变量 取在圆周K 上,点 z 在 K 的内部, 1. 0 0  − − z z z  所以 0 0 0 1 1 1 1 z z z z z − − − − = −    则 4

1 +2++++ =5-z0 是e-r ue

   + − − + − − + − = 2 0 0 0 0 0 1 ( ) ( ) 1 z z z z z z  z      + − − + n  z z z ( ) 0 0    = + − − = 0 1 0 0 ( ) . ( ) 1 n n n z z  z   − = +  −      − = 1 0 1 0 0 ( ) ( ) ( )d 2π 1 ( ) N n n K n z z z f i f z    于是         − − +  = + K n N n n z z z f i ( ) d . ( ) ( ) 2π 1 1 0 0    5