
概率论与数理统计公式全集 一、随机事件和概率 1、随机事件及其概率 运算律名称 表达式 交换律 A+B=B+A AB=BA 结合律 (A+B)+C=A+(B+C)=A+B+C (AB)C=A(BC)=ABC 分配律 AB±C)=AB±AC A+(BC)=(A+BXA+C) 德摩根律 A+B=AB 4B=4+B 2、概率的定义及其计算 公式名称 公式表达式 求逆公式 P(=1-P(A0 加法公式 P氏A+B)=PA)+PB-P氏AB) 条件概率公式 P()PAB) P(A) 乘法公式 P(AB)=P(A)P(BA)P(AB)=P(B)P(AB) 全概率公式 -4m4 贝叶斯公式 PA)PE4) P(A,B)=- (逆概率公式) 44 伯努利概型公式 P.(k)=Chp(I-p)"-k,k=0.L.n 两件事件相互独立相PAB)=PAP(B);P代A)=PB);PA=P;P)+PEA=1; 应公式 P(B)+P(B)=1
1 概率论与数理统计公式全集 一、随机事件和概率 1、随机事件及其概率 运算律名称 表达式 交换律 A+ B = B+ A AB= BA 结合律 (A+ B) +C = A+ (B +C) = A+ B +C (AB)C = A(BC) = ABC 分配律 A(B C) = AB AC A+ (BC) = (A+ B)(A+C) 德摩根律 A+ B = AB AB = A+ B 2、概率的定义及其计算 公式名称 公式表达式 求逆公式 P(A) =1− P(A) 加法公式 P(A+ B) = P(A) + P(B) − P(AB) 条件概率公式 ( ) ( ) ( ) P A P AB P B A = 乘法公式 P(AB) = P(A)P(B A) P(AB) = P(B)P(AB) 全概率公式 = = n i P B P Ai P B Ai 1 ( ) ( ) ( ) 贝叶斯公式 (逆概率公式) = = 1 ( ) ( ) ( ) ( ) ( ) i j i j j j P A P B A P A P B A P A B 伯努利概型公式 P k C p p k n k k n k n ( ) = n (1− ) − , = 0,1, 两件事件相互独立相 应公式 P(AB) = P(A)P(B) ; P(B A) = P(B) ; P(B A) = P(B A) ; P(B A) + P(B A) =1 ; P(B A) + P(B A) =1

二、随机变量及其分布 1、分布函数性质 P(X≤b)=F(b)P(a<X≤b)=F(b)-F(ad) 2、离散型随机变量 分布名称 分布律 0-1分布Lp) P(X=k)=p*(1-p)-4.k=0.1 二项分布Bm,p) P(X=k)=Chp (1-p,k=0L. 泊松分布P(2)或π(1) 风x的装=0l2 几何分布GP) PX=k)=I-p)p,k=0,12. 超几何分布HN,M,m K=利-S$C,k=+lma CN 3、连续型随机变量 分布名称 密度函数 分布函数 1 均匀分布U(a,b) f)=6-0a<x<b F) B-0a ≤x<b 0, 其他 -x2b 指数分布 B减80,A=。0>中 =ae40 Γ0,其他 正态分布N4,G),G>0 w2a -<x<+ Awa器a, D(x)= 标准正态分布N(O,1) m房。背 -0<r<+d0
2 二、随机变量及其分布 1、分布函数性质 P(X b) = F(b) P(a X b) = F(b) − F(a) 2、离散型随机变量 分布名称 分布律 0–1 分布 B(1, p) ( ) (1 ) , 0,1 1 = = − = − P X k p p k k k 二项分布 B(n, p) P X k C p p k n k k n k n ( = ) = (1− ) , = 0,1, , − 泊松分布 P()或() , 0,1,2, ! ( = ) = = − k k P X k e k 几何分布 G( p) P(X = k) = (1− p) k−1 p, k = 0,1,2, 超几何分布 H(N,M,n) ( ) , k l,l 1, ,min( n,M ) C C C P X k n N n k N M k = = M = + − − 3、连续型随机变量 分布名称 密度函数 分布函数 均匀分布 U (a,b) = − 0, 其他 , 1 ( ) a x b f x b a − − = x b a x b b a x a x a F x 1, , 0, ( ) 指数分布 ( 0) 1 ( )或 ( ), = E E = − 0, 其他 , 0 ( ) e x f x x − = − 1 , 0 0, 0 ( ) e x x F x x 正态分布 ( , ), 0 2 N = − + − − f x e x x 2 2 2 ( ) 2 1 ( ) − − − = x t F x e d t 2 1 ( ) 2 2 2 ( ) 标准正态分布 N(0,1) = − + − x e x x 2 2 2 1 ( ) − − − = x t x e dt 2 1 ( ) 2 2 2 ( )

三、多维随机变量及其分布 1、离散型二维随机变量边缘分布 P=PX=)=∑PX=Y=y)=∑Pg p=PW=y)=∑PX=,Y=y)=∑P 2、离散型二维随机变量条件分布 P=x=水==PX-=2.=2 P(Y=y P%=AT-yK=-是/=2 P(X=x) 3、连续型二维随机变量(X,P)的联合分布函数Fx,)=∫fu,d 4、连续型二维随机变量边缘分布函数与边缘密度函数 边缘分布函数:Fx()=广fu,dha边缘密度函数:r)=fxd F)=[f(u.v)dudv f(y)=[f(u.y)du 5、二维随机变量的条件分布 m0器nmwn8en
3 三、多维随机变量及其分布 1、离散型二维随机变量边缘分布 = = = = = = j j i i i j pij p P(X x ) P(X x ,Y y ) = = = = = = i i j j i j pij p P(Y y ) P(X x ,Y y ) 2、离散型二维随机变量条件分布 , 1,2 ( ) ( , ) ( ) = = = = = = = = = i P p P Y y P X x Y y p P X x Y y j ij j i j i j i j , 1,2 ( ) ( , ) ( ) = = = = = = = = = j P p P X x P X x Y y p P Y y X x i ij i i j j i j i 3、连续型二维随机变量( X ,Y )的联合分布函数 − − = x y F(x, y) f (u,v)dvdu 4、连续型二维随机变量边缘分布函数与边缘密度函数 边缘分布函数: − + − = x FX (x) f (u,v)dvdu 边缘密度函数: + − f x = f x v dv X ( ) ( , ) − + − = y FY (y) f (u,v)dudv + − fY ( y) = f (u, y)du 5、二维随机变量的条件分布 = − y + f x f x y f y x X Y X , ( ) ( , ) ( ) = − x + f y f x y f x y Y X Y , ( ) ( , ) ( )

四、随机变量的数字特征 1、数学期望 离散型随机变量:B)=之:连续型随机变量:B()-达 2、数学期望的性质 (1)E(C=C,c为常数 (X=E(X)E(CX)=CE(X) (②)EX±n=Ex)±E(Y)E(ax±=a0±bEGX+.C,X,)=CX)+C,EX,) (3)若X,Y相互独立则:)=x) (4)IE(XF sE(xE) 3、方差计算公式:D(X)=Ex)-E2() 4、方差的性质 (1)D(C)=0 DD(X)1=0 D(ax+b)=aD(x)DX)<E(X-C) (②)Dx±n=0+Dmt2Cmx,n若X,Y相互独立则:Dx±n=D)+Dn 5、协方差:Com(X,)=EX,)-EXE)若X,Y相互独立则:ComX,)=0 6、相关系数:n品若,Y相互發立则:即V不相关 7、协方差和相关系数的性质 (1)CoMx.X)=D(X)CoMX.r)=ConY.x) (2)CorXj+X2.Y)=CorX1.Y)+CoMX2.Y)Cor(aX+c.bY+d)=abCoMX.Y)
4 四、随机变量的数字特征 1、数学期望 离散型随机变量: + = = 1 ( ) k k pk E X x 连续型随机变量: + − E(X ) = xf (x)dx 2、数学期望的性质 (1) E(C) = C,C为常数 E[E(X)] = E(X) E(CX) = CE(X) (2) E(X Y) = E(X) E(Y) E(aX b) = aE(X) b ( ) ( ) ( ) E C1X1 +CnXn = C1E X1 +CnE Xn (3)若 X,Y 相互独立则: E(XY) = E(X)E(Y) (4) [ ( )] ( ) ( ) 2 2 2 E XY E X E Y 3、方差计算公式: ( ) ( ) ( ) 2 2 D X = E X − E X 4、方差的性质 (1) D(C) = 0 D[D(X)] = 0 ( ) ( ) 2 D aX b = a D X 2 D(X) E(X −C) (2) D(X Y) = D(X) + D(Y) 2Cov(X,Y) 若 X,Y 相互独立则: D(X Y) = D(X) + D(Y) 5、协方差: Cov(X,Y) = E(X,Y) − E(X)E(Y) 若 X,Y 相互独立则: Cov(X,Y) = 0 6、相关系数: ( ) ( ) ( , ) ( , ) D X D Y Cov X Y XY = X Y = 若 X,Y 相互独立则: XY = 0 即 X,Y 不相关 7、协方差和相关系数的性质 (1) Cov(X, X) = D(X) Cov(X,Y) = Cov(Y, X) (2) ( , ) ( , ) ( , ) Cov X1 + X2 Y = Cov X1 Y +Cov X2 Y Cov(aX + c,bY + d) = abCov(X,Y)
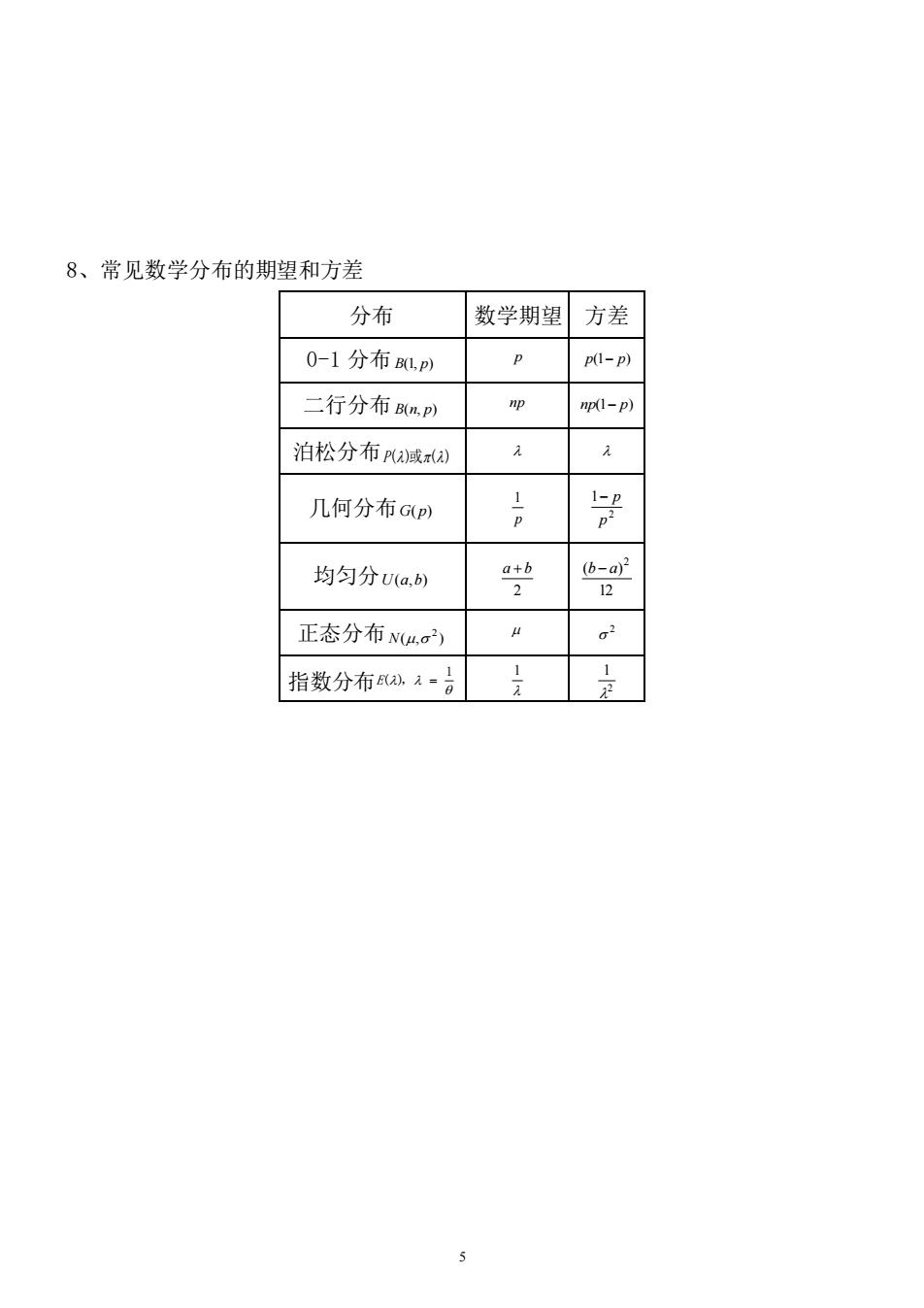
8、常见数学分布的期望和方差 分布 数学期望方差 0-1分布1P) P(l-p) 二行分布BmP) m1-p) 泊松分布减a) 几何分布Gp) 导 均匀分Ua,b) 正态分布N4,a 02 指数分布元-日 5
5 8、常见数学分布的期望和方差 分布 数学期望 方差 0-1 分布 B(1, p) p p(1− p) 二行分布 B(n, p) np np(1− p) 泊松分布 P()或() 几何分布 G( p) p 1 2 1 p − p 均匀分 U(a,b) 2 a + b 12 ( ) 2 b − a 正态分布 ( , ) 2 N 2 指数分布 1 E( ), = 1 2 1