
第二节柯西古萨定理及其推广 一、问题的提出 二、柯西古萨定理及其推广 三、典型例题 四、原函数和不定积分
第二节柯西古萨定理及其推广 一、问题的提出 二、柯西古萨定理及其推广 三、典型例题 四、原函数和不定积分

问题的提出 研究复积分与路径的无关性: 目的 由上节例受到的启发→积分与路径无关与函数 沿着围线的积分值为零有何关系 首先:若复积分与路径无关,则对任意围线C, 在其上任取两点按a(起点),b(终点) 将曲线C分成两部分C=C1+C2 因为积分与路径无关,所以: cf(z)d=∫f(z)dk →∫cf(z)d=Jf(z)k-∫6,f(z)k=0
一、问题的提出 C C1 C2 目的 研究复积分与路径的无关性: 由上节例受到的启发积分与路径无关与函数 沿着围线的积分值为零有何关系 首先:若复积分与路径无关,则对任意围线C, 在其上任取两点按a(起点),b(终点) b a C C2 C1 将曲线C分成两部分 因为积分与路径无关,所以: 1 2 ( ) ( ) C C f z dz f z dz 1 2 ( ) ( ) ( ) 0 C C C f z dz f z dz f z dz 2

二、基本定理 定理3.2(柯西积分定理): 如果函数f(z)在单连通域D内处处解析,那 末函数f(z)沿D内的任何一条简单闭线C积 分为零: f(=)d-=0. 此定理也称为柯西古萨定理。 定理的证明
B 二、基本定理 定理3.2(柯西积分定理): ( )d 0. ( ) ( ) c f z z f z D C f z 分为零: 末函数 沿 内的任何一条简单闭曲线 积 如果函数 在单连通域 D 内处处解析,那 C 此定理也称为柯西古萨定理. 定理的证明 3

关于定理3.2的说明: (1) 定理3.3设函数f(z)在单连通区域D内解析,z。与 z为D内的任意两点,C与C,为连结z。与z的积分 曲线,C与C,都含于D内,则 重fa=重fe比 即当f(z)为D的解析函数时,积分与路径无关, 而仅由积分路线的起点z和终点z,有关
f z dz f z dz c c 1 2 ( ) ( ) 曲线, 与 都含于 内,则 为 内的任意两点, 与 为连结 与 的积分 定理3.3设函数 在单连通区域 内解析, 与 C C D z D C C z z f z D z 1 2 1 1 2 0 1 0 ( ) 而仅由积分路线的起点 和终点 有关。 即当 为 的解析函数时,积分与路径无关, 0 1 ( ) z z f z D 关于定理3.2的说明: 4 (1)
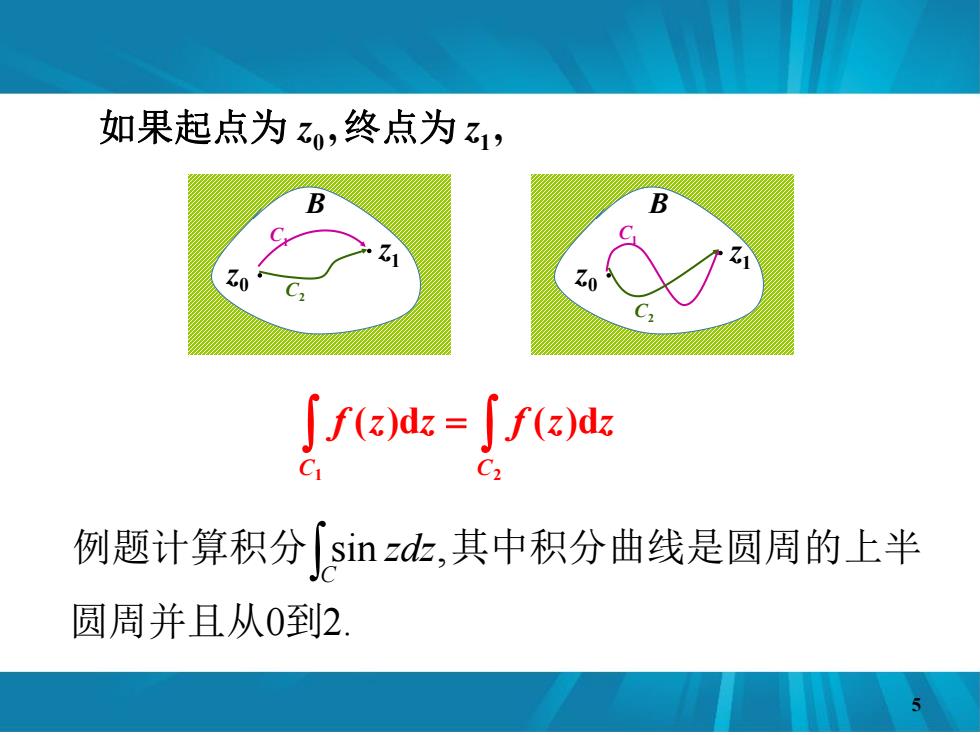
如果起点为z0,终点为乙1, Zo fry-frd C, 例题计算积分sinzd,其中积分曲线是圆周的上半 圆周并且从0到2
B B 0 z 1 z 0 z 1 z C1 C2 C1 C2 , , 0 1 如果起点为 z 终点为 z 1 2 ( )d ( )d C C f z z f z z 0 2.sin , 圆周并且从 到 例题计算积分 其中积分曲线是圆周的上半 C zdz 5