
第四节洛朗级数 一、问题的引入 二、洛朗级数的概念 三、函数的洛朗展开式 四、典型例题 五、小结与思考
第四节洛朗级数 二、洛朗级数的概念 一、问题的引入 三、函数的洛朗展开式 五、小结与思考 四、典型例题

一、问题的引入 在圆环域内解析的函数是否一定能展开成级数? 例如,fa)= 1 在z=0及z=1都不解析, z(1-z) 但在圆环域0<z<1及0<z-1<1内都是解析的. 在圆环域0<z<1内: (a)- 1 1,1 =z0-02+1-2 而 1=1+z+z2++z”+,z<1 1-
在圆环域 0 z 1内: 例如, 0 1 (1 ) 1 ( ) = = − = z z z z f z 在 及 都不解析, 但在圆环域 0 z 1 及 0 z − 1 1 内都是解析的. (1 ) 1 ( ) z z f z − = 而 1 , 1 1 1 2 = + + + + + − z z z z z n 在圆环域内解析的函数是否一定能展开成级数? , 1 1 1 z − z = + 2 一、问题的引入

所以f(z)= z(1-z) =z1+1+z+z2+.+z”+., 即f(z)在0<z<1内可以展开成级数, 在圆环域0<z-1<1内,也可以展开成级数: a02g[-】 =1+0-+0-++1-+ =(1-z)+1+(1-z)+(1-z)2+(1-z)”-1+
所以 (1 ) 1 ( ) z z f z − = 1 , = z −1 + + z + z 2 ++z n + 即 f (z)在 0 z 1 内可以展开成级数. 在圆环域0 z −1 1内, 也可以展开成级数: (1 ) 1 ( ) z z f z − = − − − = 1 (1 ) 1 1 1 z z + − + − ++ − + − = n z z z z 1 (1 ) (1 ) (1 ) 1 1 2 (1 ) 1 (1 ) (1 ) (1 ) . = − z −1 + + − z + − z 2 + − z n−1 +

00 2.双边幂级数∑cn(z-zo)” 觅ce-4r cn(z-zo) Cn(z-z)” n=」 1=-00 2=0 负幂项部分 正幂项部分 收敛 主要部分 解析部分 同时收敛
n n n 2. c (z z ) − 0 =− 双边幂级数 负幂项部分 正幂项部分 主要部分 解析部分 同时收敛 收敛 − = = =− n n n n c (z z ) 0 n n n n n n c (z z ) c (z z ) 0 0 0 1 − + − = − = − 4
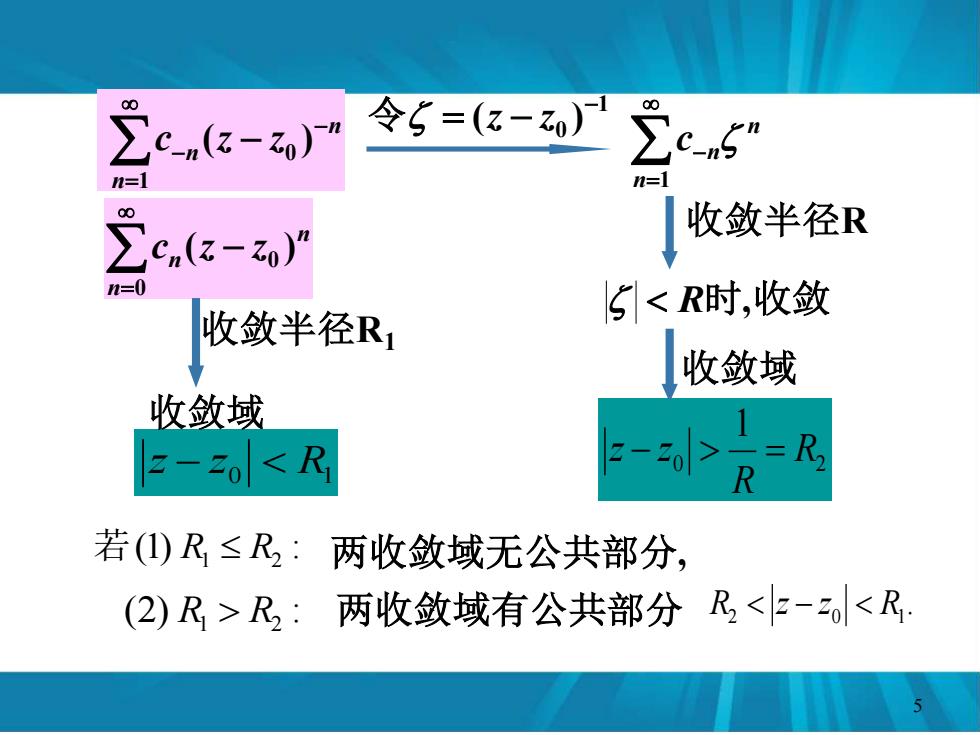
∑cn-) 令5=(z-0) 00 n=1 =1 00 收敛半径R Cn(z-z)” 1≥0 收敛半径R1 5<R时,收敛 收敛域 收敛域 2-o<R =R R 若()R≤R:两收敛域无公共部分, (2)R>R2:两收敛域有公共部分R<-<R
n n n c (z z ) 0 0 − = n n n c z z − = − ( − ) 0 1 1 0 ( ) − 令 = z − z n n n c = − 1 收敛半径R R时,收敛 0 2 1 R R z − z = 收敛域 收敛半径R1 0 R1 z − z 收敛域 (1) : 若 R1 R2 两收敛域无公共部分, (2) : R1 R2 两收敛域有公共部分 . 2 0 R1 R z − z 5