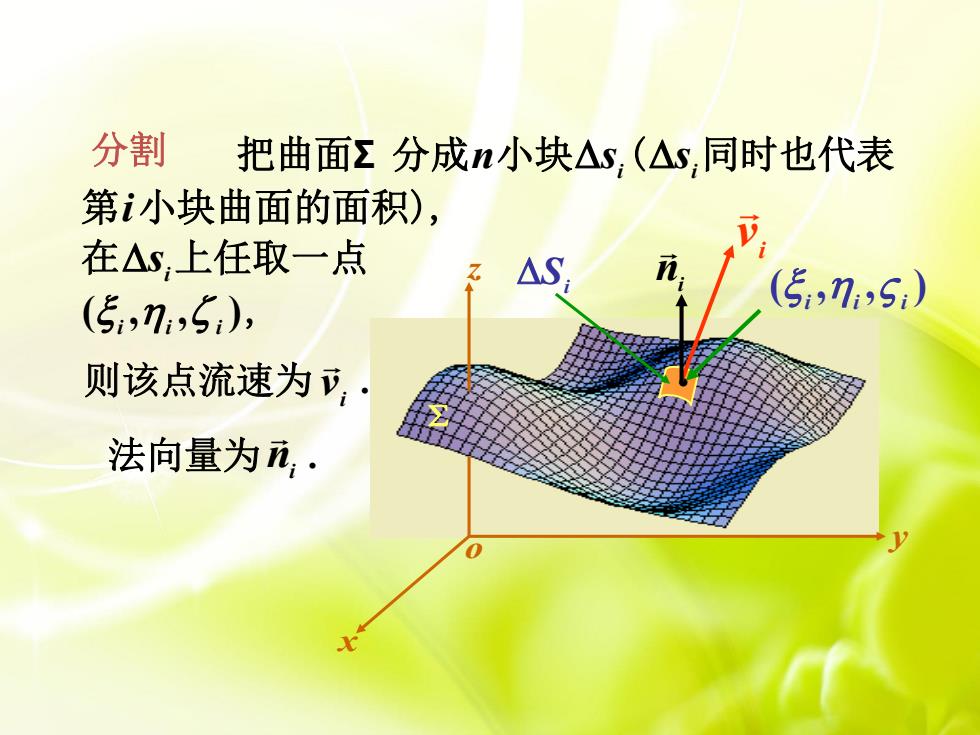
分割 把曲面Σ分成n小块△s,(△s,同时也代表 第i小块曲面的面积), 在△S,上任取一点 子△S (5,7,5), (5,135) 则该点流速为立,· 法向量为元·
x y z o Si ( , , ) i i i i v ni 把曲面Σ 分成n小块 i s ( i s 同时也代表 第i小块曲面的面积), 在 i s 上任取一点 ( , , ) i i i , 分割 则该点流速为 . i v 法向量为 . ni

=(5,7,5) =P(5,n,5)i+2(5,n,5)j+R(5,n,5)k, 该点处曲面Σ的单位法向量 n=cosa,i+cosBj+cosy,k, 近似求和通过△S,流向指定侧的流量近似值为 可·△S,(i=1,2,.,m. 通过Σ流向指定侧的流量 D≈∑可AS
该点处曲面Σ 的单位法向量 ni i i i j ik cos cos cos 0 , 0 ( 1,2, , ). i i i v n S i n ( , , ) ( , , ) ( , , ) , ( , , ) P i Q j R k v v i i i i i i i i i i i i i 近似求和 0 1 n i i i i v n S 通过Si流向指定侧的流量近似值为 通过Σ流向指定侧的流量

=∑IP(5i,n,5,)c0sa,+0(5,n,5:)cos月 +R(,5:)cosY;lAS, =∑IP(5,n,5△S,)R+2(5,5AS)x i- +R(5,7,5)△S)x 取极限入→0时取极限得到流量Φ的精确值. D=21P55as)+05,5》 +R(5,7,5)(△S)g]
1 [ ( , , )cos ( , , )cos ( , , )cos ] n i i i i i i i i i i i i i i P Q R S ( , , )( ) ] [ ( , , )( ) ( , , )( ) 1 i i i i x y yz i i i i x z n i i i i i R S P S Q S 取极限 0 . 时取极限得到流量 的精确值 ( , , )( ) ] lim [ ( , , )( ) ( , , )( ) 1 0 i i i i x y yz i i i i x z n i i i i i R S P S Q S

2、概念 定义设Σ为光滑的有向曲面,函数在Σ上有 界,把∑分成n块小曲面△S:(△S,同时又表示第i 块小曲面的面积),△S,在x0y面上的投影为 (△S)xy,(5,7,5i)是△S,上任意取定的一点,如 果当各小块曲面的直径的最大值入→0时, Iim∑R(5,n,5)(△S:)w →0=1 则称此极限为函数R(x,y,z)在有向曲面Σ上 对坐标xy的曲面积分(也称第二类曲面积分)
定义 设 Σ 为光滑的有向曲面,函数在 Σ 上有 界,把 Σ 分成n块小曲面Si (Si同时又表示第i 块小曲面的面积), Si 在 xoy 面上的投影为 Si xy ( ) ,( , , ) i i i 是Si上任意取定的一点,如 果当各小块曲面的直径的最大值 0时, n i R i i i Si xy 1 0 lim ( , , )( ) 则称此极限为函数R(x, y,z)在有向曲面Σ 上 对坐标 x,y 的曲面积分(也称第二类曲面积分) 2、概念

记作∬R(x,y,z)dcd,即 JRs3=m∑R(5,n:5,XASw i=1 被积函数 积分曲面 类似可定义 J∬P(c,yz)ddt=lim∑P(5n,5,(△S,)e →0 i1 (x,z)tkk=lm∑0(5,n,5,(△S)a 2→0 i=1
记作 R( x, y,z)dxdy,即 n i R i i i Si x y R x y z dxdy 1 0 ( , , ) lim ( , , )( ) 被积函数 积分曲面 类似可定义 n i P i i i Si yz P x y z dydz 1 0 ( , , ) lim ( , , )( ) n i Q i i i Si zx Q x y z dzdx 1 0 ( , , ) lim ( , , )( )