
下册目录 第八章向量代数与空间解析几何 习照8向层及其线性 积混合积 方程 习85曲面及其方 习题8-6空间曲线及其方程 总习题八 第九章多元函数微分法及其应用 习题91多元函数的基本概念 习题9-2 偏导数 习题9-3 习题9 :元复合函数的求导法则 向数微 学的几何应用 习题8多元函数的极值及其求法 习题0.0 元函数的泰勒公式 习题910最小二乘法 总习题九 第十章重积分 习题10-1 二重积分的概念与性质 习题10-2 二重积分的计算法 习题10-3 总习题十 秋的分 第十一章曲线积分与曲面积分 习题111对弧长的曲线积分 习题11-2对坐标的曲线积分 习题3格林公式及其应用 习题114对面积的曲面积分 习题11-5 对坐标的曲面积分 习题11-6 习题121常数项级数的概念和性质 习题12-2常数项级数的审敛法 习题12-3 系级数 习题12-4 函数展开成幂级数 习题125函数的幂级数展开式的应用 习题12-6函数项级数的一致收敛性及一致收敛级数的基本性质 习题12-7 傅里叶级数 一般周期函数的傅里叶级数
下册目录 第八章 向量代数与空间解析几何 习题 8-1 向量及其线性运算 习题 8-2 数量积 向量积 混合积 习题 8-3 平面及其方程 习题 8-4 空间直线及其方程 习题 8-5 曲面及其方程 习题 8-6 空间曲线及其方程 总习题八 第九章 多元函数微分法及其应用 习题 9-1 多元函数的基本概念 习题 9-2 偏导数 习题 9-3 全微分 习题 9-4 多元复合函数的求导法则 习题 9-5 隐函数的求导公式 习题 9-6 多元函数微分学的几何应用 习题 9-7 方向导数与梯度 习题 9-8 多元函数的极值及其求法 习题 9-9 二元函数的泰勒公式 习题 9-10 最小二乘法 总习题九 第十章 重积分 习题 10-1 二重积分的概念与性质 习题 10-2 二重积分的计算法 习题 10-3 三重积分 习题 10-4 重积分的应用 习题 10-5 含参变量的积分 总习题十 第十一章 曲线积分与曲面积分 习题 11-1 对弧长的曲线积分 习题 11-2 对坐标的曲线积分 习题 11-3 格林公式及其应用 习题 11-4 对面积的曲面积分 习题 11-5 对坐标的曲面积分 习题 11-6 高斯公式 通量与散度 习题 11-7 斯托克斯公式 环流量与旋度 总习题十一 第十二章 无穷级数 习题 12-1 常数项级数的概念和性质 习题 12-2 常数项级数的审敛法 习题 12-3 幂级数 习题 12-4 函数展开成幂级数 习题 12-5 函数的幂级数展开式的应用 习题 12-6 函数项级数的一致收敛性及一致收敛级数的基本性质 习题 12-7 傅里叶级数 习题 12-8 一般周期函数的傅里叶级数 总习题十二

第八章 向量代数与空间解析几何 习题8-1 向量及其线性运算 21.设w=a-b+2c,v=-a+3b-c.试用a,b,c表示2u-3u. 解2u-3)=2(a-b+2c)-3(-a+3b-c) =5a-11b+7c. 2.如果平面上一个四边形的对角线互相平分,试用向量证明它是平行四边形 证如图8-1,设四边形ABCD中AC与BD交于点M,已知Ai=MC.D=ME A店=Ai+店=M元+D丽=D元 即AB∥DC且|AB|=|DC|.因此四边形ABCD是平行四边形 图8-1 图8-2 ☑3.把△ABC的BC边五等分,设分点依次为D1,D2,D,D4,再把各分点与点A连接 试以AB=c.BC=a表示向量D,.DA,D和D4A. 证如图8-2,根据题意知 D={a,=a,D,=a,D=了a, ,=-(店+BD)=-5a-C p,=-(ai+B)=-5a-C ,A=-(Ai+BD)=-了a-C

4 一、《高等数学》(第七版)下册习题全解 D4i=-(Ag+BD)=-专a-c ☑4.已知两点M,(0,1,2)和M2(1,-1,0).试用坐标表示式表示向量M,及 -2M1M2 解M,M=(1-0,-1-1,0-2)=(1,-2,-2) -2M1M3=-2(1,-2.-2)=(-2.4,4). 25.求平行于向量a=(6,7,-6)的单位向量 解向量▣的单位向量为日,故平行于向量口的单位向量为 日6,7-6)=品7 其中|a|=√62+72+(-6)2=11. 忍6.在空间直角坐标系中,指出下列各点在哪个卦限? A(1,-2.3),B(2.3,-4).C(2,-3.-4).D(-2.-3.1) 解A点在第四卦限,B点在第五卦限,C点在第八卦限,D点在第三卦限。 7.在坐标面上和在坐标轴上的点的坐标各有什么特征?指出下列各点的位置 A(3.4.0),B(0.4.3).C(3.0.0).D(0.-1.0). 解在坐标面上的点的坐标,其特征是表示坐标的三个有序数中至少有一个为 零.比如x0y面上的点的坐标为(x00,0),x0:面上的点的坐标为(x00,0)0:面 上的点的坐标为(0,yo,0). 在坐标轴上的点的坐标,其特征是表示坐标的三个有序数中至少有两个为零。 比如x轴上的点的坐标为(x0,0,0)y轴上的点的坐标为(0,o.0):轴上点的坐标 为(0,0,0) A点在xO,面上,B点在O:面上,C点在x轴上,D点在y轴上. ☑8.求点(,b,c)关于(1)各坐标面:(2)各坐标轴:(3)坐标原点的对称点的 坐标. 解(I)点(a,b,c)关于xO面的对称点为(a,b,-c),关于:面的对称点是 (-a,b,c),关于0x面的对称点为(a,-b,c). (2)点(a,b,c)关于x轴的对称点是(a.-6,-).关于y轴的对称点是(-u b,-c),关于:轴的对称点是(-a,-b.c). (3)点(a,b,c)关于坐标原点的对称点是(-,-b,-c) 9.自点P(0,)分别作各坐标面和各坐标轴的垂线.写出各垂足的坐怀。 解设空间直角坐标系如图8-3.根据题意.P,F为点P。关于:面的垂线 垂足F坐标为(xo,0,n):PD为点P。关于仍面的垂线.垂足D坐怀为(n。.0): PE为点P。关于:面的垂线,垂足E坐标为(0.an) PaA为点P,关于x轴的垂线,垂足A的坐标为(0.0):PB为点P。关于,轴
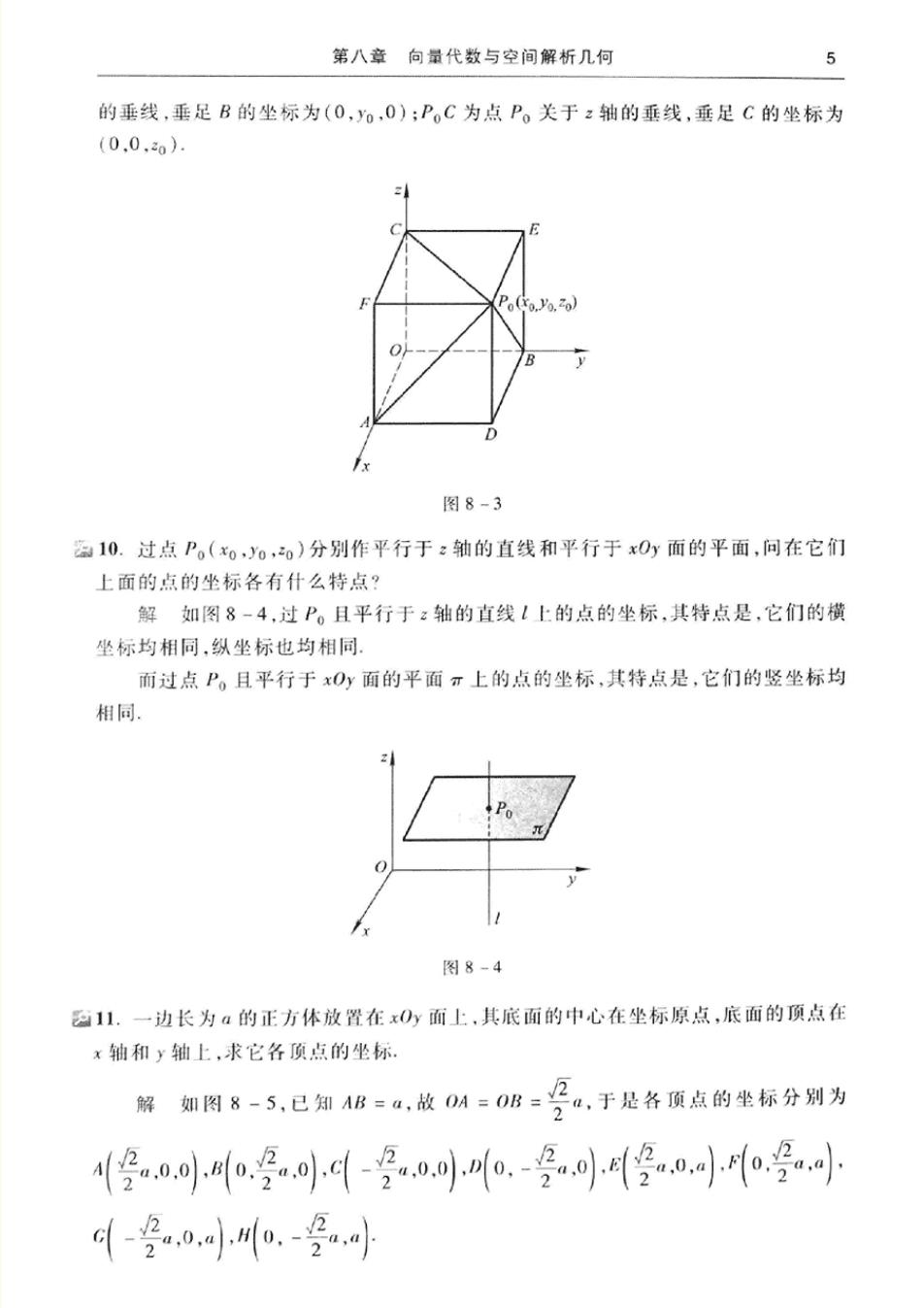
第八章向量代数与空间解析几何 的垂线,垂足B的坐标为(0,o,0):P。C为点P。关于z轴的垂线,垂足C的坐标为 (0.0.o) 图8-3 10.过点P,(00,o)分别作平行于:轴的直线和平行于x0y面的平面,问在它们 上面的点的坐标各有什么特点? 解如图8-4,过P。且平行于:轴的直线1上的点的坐标,其特点是,它们的横 坐标均相同,纵坐标也均相同. 而过点P。且平行于xOy面的平面π上的点的坐标,其特点是,它们的竖坐标均 相同. 图8-4 11.一边长为a的正方体放置在x面上,其底面的中心在坐标原点,底面的顶点在 x轴和y轴上,求它各顶点的坐标 解如图8-5,已知AB=a,故0A=0B=a,于是各顶点的坐标分别为 4.o-o.0.-小0小号 -号.小o9小

6 一、《高等数学》(第七版)下册习题全解 图8-5 12.求点M(4,-3,5)到各坐标轴的离. 解点M到x轴的距离山1=√(-3)2+52=34,点W到y轴的距离小2 √42+57=√41.点M到:轴的距离d=√42+(-3)下=√/25=5. 213.在y0:面上,求与三点A(3.1,2),B(4,-2,-2)和C(0.5,1)等距离的点. 解所求点在y0:面上,不妨设为P(0,y),点P与三点A,B.C等距离, |P|=√32+(y-1)2+(:-2)下.1Pg|=√43+(y+2)+(:+2)2 1P元|=√(y-5)2+(:-1) 由|P|=|P店|=P元|知 √32+(y-1)2+(:-2)2=42+(0+2)2+(:+2)2=√(y-5)2+(:-1)2 即 9+(y-1)2+(:-2)2=16+(y+2)2+(:+2)2 19+(y-1)2+(:-2)2=(y-5)2+(:-1)2 解上述方程组,得y=1,:=-2.故所求点坐标为(0.1.-2). 14.试证明以三点A(4.1.9),B(10.-1.6).C(2.4.3)为顶点的三角形是等腰直角 三角形. 证由|AB|=√(10-4)2+(-1-1)2+(6-9)2=7. 11=√(2-4)2+(4-1)2+(3-9)2=7. |BC|=√/(2-10)2+(4+1)'+(3-6)=98=75 知M店=AC1及B配12=1A2+AC12.放△ABC为等胶直角三角形 ☑15.设已知两点M,(4.2.1)和M,(3.0.2).计算向量1,1的模.方向余弦和方 向角. 解向量 M,M=(3-4.0-2.2-1)=(-1.-2.1)