
二、罗尔(Rolle)定理罗尔1652年4月21日出生于昂贝尔特的一个小店家庭,因家境贫困,只受过初等教育。罗尔在数学上的成就主要是在代数方面,专长于丢番图方程的研究。1682年他解决了数学家奥扎南提出的一个数论难题,从而名身雀起,也使他的生活有了转机。他担任过初等数学教师和陆军部行征官员。1685年进入法国科学院担任低级职务,到罗尔1690年才获得科学院发给的固定薪水,此后他一直在科学院供职。 1719年11 月8日因中Rolle风卒于巴黎。罗尔于1691年在题为 《任意次方程的一1652-1719个解法的证明》的论文中指出了:在多项法国数学家式方程的两个相的实根之间,方程至少有一个根。一百多年后,即1846年,尤斯托·伯拉维提斯将这一定理推广到可微函数,并把此定理命名为罗尔定理
罗尔1652年4月21日出生于昂贝尔特的一 个小店家庭,因家境贫困,只受过初等教 育。罗尔在数学上的成就主要是在代数方 面,专长于丢番图方程的研究。1682年, 他解决了数学家奥扎南提出的一个数论难 题, 从而名身雀起, 也使他的生活有了转机。 他担任过初等数学教师和陆军部行征官员。 1685年进入法国科学院担任低级职务,到 1690年才获得科学院发给的固定薪水,此 后他一直在科学院供职。1719年11月8日因中 风卒于巴黎。 罗尔于1691年在题为《任意次方程的一 个解法的证明》的论文中指出了:在多项 式方程的两个相邻的实根之间,方程 至少 有一个根。一百多年后,即1846年,尤斯 托﹒伯拉维提斯将这一定理推广到可微函 数,并把此定理命名为罗尔定理。 罗 尔 Rolle 1652-1719 法国数学家 二、罗尔(Rolle)定理

罗尔(Rolle)定理如果函数f(x)满足(1)在闭区间[a,b]|上连续(2)在开区间(a,b)内可导;(3)在区间端点处的函数值相等,即f(a)= f(b),那么在(a,b)内至少有一点 (a<<b),使得f'()= 0.例如, f(x)= x2 -2x-3=(x-3)(x+1)在[-1,3]上连续,在(-1,3)上可导,且 f(-1) = f(3) = 0, : f'(x)= 2(x -1),取=1, (1e(-1,3))f'()= 0
例如, 2 f x x x x x ( ) 2 3 ( 3)( 1). = − − = − + 在[−1,3]上连续, 在(−1,3)上可导, 且 f (−1) = f (3) = 0, 取 = 1, (1(−1,3)) f () = 0. f (x) = 2(x − 1), ( ) (1) [ , ] ; (2) ( , ) ; (3) , ( ) (Rol ( ), ( , ) ( le ), ( ) 0. ) f x a b a b f a f b a b a b f = = 如果函数 满足 在闭区间 上连续 在开区间 内可导 在区间端点处的函数值相等 即 那么在 内至少有一点 使得 罗尔 定理
V几何解释:y= f(x)在曲线弧AB上至少有一点C,在该点处的切线是5152水平的,即为驻点0bxa
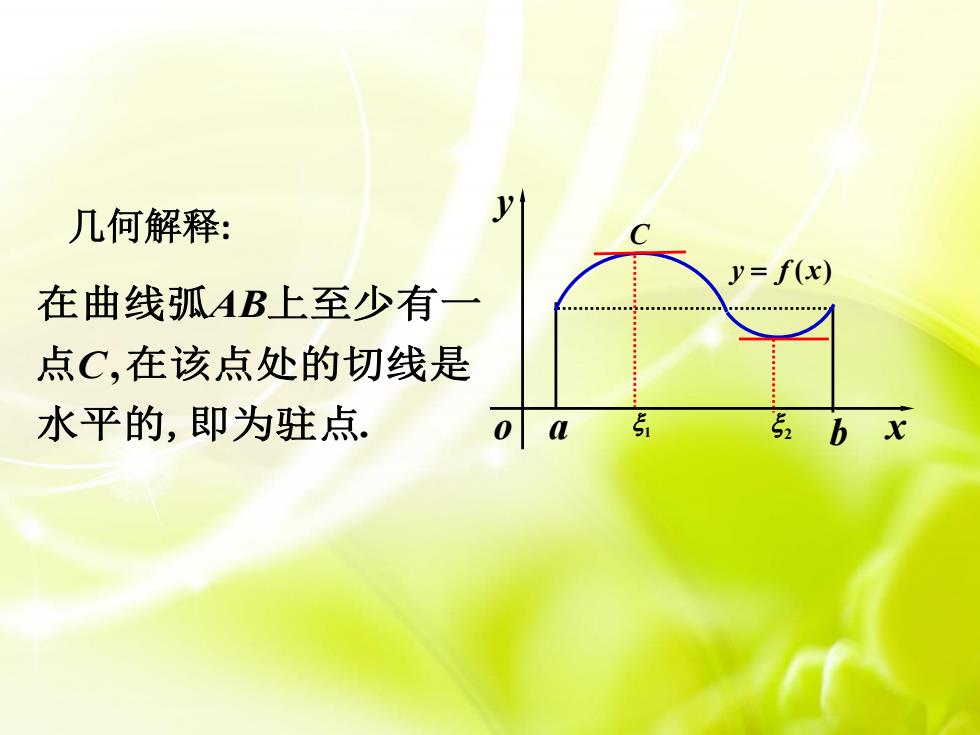
几何解释: a 1 b 2 x y o y = f (x) , . AB C 在曲线弧 上至少有一 点 在该点处的切线是 水平的,即为驻点 C

证::f(x)在[a,b]连续,必有最大值 M 和最小值 m.(1)若 M =m. 则 f(x)= M.由此得 f'(x)=0. V (a,b),都有 f()=0.(2)若 M ±m. : f(a) = f(b),.最值不可能同时在端点取得设 M ± f(a),则在 (a,b)内至少存在一点 使 f(5) = M.因此,VxE[a,b],f(x)≤f(),由费马引理可知f'(5) =0
证: (1) 若 M = m. f (x) 在[a,b]连续, 必有最大值 M 和最小值 m. 则 f x M ( ) . 由此得 f (x) = 0. = ( , ), ( ) . a b f 都有 0 (2) 若 M m. f (a) = f (b), 最值不可能同时在端点取得. ( ), ( , ) ( ) . M f a a b f M = 设 则在 内至少存在一点 使 , [ , ], ( ) ( ), ( ) 0. x a b f x f f = 因此 由费马引理可知

注意:若罗尔定理的三个条件中有一个不满足V其结论可能不成立例如:y =x|,x E[-2,2];在[-2,2]上除 f'(0)不存在外,满足罗尔定理的一切条件,但在区间「一2,21内找不到一点能使 f'(x) = 0.1-x, xe(0,1)又如:=0, x=0y = x, xe[0,1]
➢ 注意:若罗尔定理的三个条件中有一个不满足, 其结论可能不成立. 例如:y x x = − , [ 2,2]; [ 2,2] (0) , , [ 2 2] ( ) 0. f f x − − = 在 上除 不存在外 满足罗尔定理 的一切条件 但在区间 , 内找不到一点能 使 1 , (0,1] ; 0, 0 x x y x − = = 又如: y = x, x [0,1]