
第四节函数的单调性与曲线的凹凸性、单调性的判别法二、曲线的凹凸性与拐点三、小结
第四节 函数的单调性 与曲线的凹凸性 • 一、单调性的判别法 • 二、曲线的凹凸性与拐点 • 三、小结
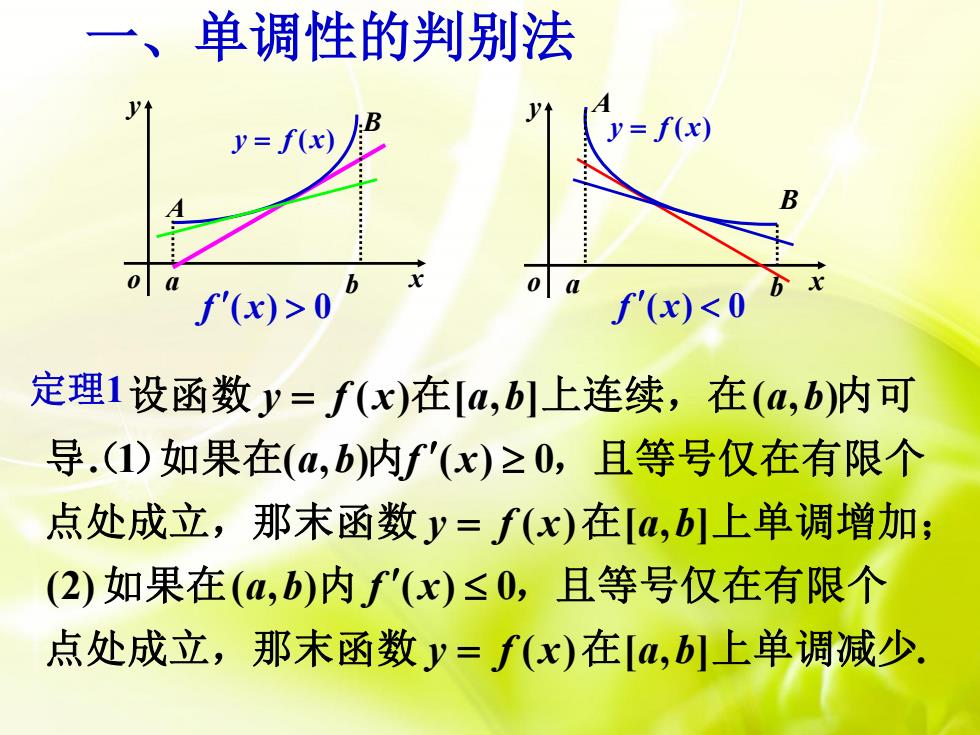
一、单调性的判别法yy= f(x)y= f(x)B0xXb0f'(x)<0f'(x)>0定理1设函数=f(x)在[a,b]上连续,在(a,b)内可导.(1)如果在(a,b)内f'(x)≥0,且等号仅在有限个点处成立,那末函数y=f(x)在[a,b]上单调增加;(2)如果在(a,b)内 f(x)≤0,且等号仅在有限个点处成立,那末函数y= f(x)在[a,b]上单调减少
一、单调性的判别法 x yo y = f (x) x y o y = f (x) a b A B f x ( ) 0 f x ( ) 0 定理1 ( ) [ , ] ( , ) . 1 ( , ) ( ) 0 ( ) [ , ] (2) ( , ) ( ) 0 ( ) [ , ] . y f x a b a b a b f x y f x a b a b f x y f x a b = = = 设函数 在 上连续,在 内可 导( )如果在 内 ,且等号仅在有限个 点处成立,那末函数 在 上单调增加; 如果在 内 ,且等号仅在有限个 点处成立,那末函数 在 上单调减少 a b B A

证 xj,x, E (a,b), 且 x, <x2, 应用拉氏定理,得(xi<≤<x2)f(x)-f(x)= f'()(x2 -x):x-x>0,若在(a,b)内,f'(x)>0,则 f'()>0,: f(x2)>f(x). :. y=f(x)在[a,b]上单调增加若在(a,b)内,f(x)<0,则 f'()<0,:. f(x)< f(x) : y= f(x)在[a,b]上单调减少
证 , ( , ), 1 2 x x a b , 1 2 且 x x 应用拉氏定理,得 ( ) ( ) ( )( ) ( ) 2 1 2 1 1 2 f x − f x = f x − x x x 0, x2 − x1 若在(a,b)内,f (x) 0, 则 f ( ) 0, ( ) ( ). 2 1 f x f x y = f (x)在[a,b]上单调增加. 若在(a,b)内,f (x) 0, 则 f ( ) 0, ( ) ( ). 2 1 f x f x y = f (x)在[a,b]上单调减少

例1 判断函数y=x-sin x在[0,2元[上的单调性解:因为在(0,2元)内y'=1-cosx> 0所以由定理1可知,函数y=x-sinx在上[0,2元单调增加
例1 sin [0,2 ] 判断函数y x x = − 在 上的单调性. 0,2 1 cos 0 1 sin [0,2 ] y x y x x = − = − 解:因为在( )内 所以由定理 可知,函数 在上 单调增加

例2讨论函数y=e*-x-1的单调性解 : y'= e* -1.又:: D:(-00,+o0).2.5N在(-80,0)内,y' < 0,1.50.54:在(-80,0]上函数单调减少;-2120.5在(0,+)内,'>0,:.在[0,+)上函数单调增加注意:函数的单调性是一个区间上的性质,要用导数在这一区间上的符号来判定,而不能用一点处的导数符号来判别一个区间上的单调性
例2 解 1 . x 讨论函数y e x = − − 的单调性 = − 1. x y e 在(−,0)内, y 0, − 在( ,0]上函数单调减少; 在(0,+)内, y 0, 在[0, ) . + 上函数单调增加 注意:函数的单调性是一个区间上的性质,要用 导数在这一区间上的符号来判定,而不能用一 点处的导数符号来判别一个区间上的单调性. 又 D :(−,+)