
第六节高阶线性微分方程一、概念的引入二、 线性微分方程的解的结构三、小结
第六节 高阶线性微分方程 • 一、概念的引入 • 二、线性微分方程的解的结构 • 三、小结
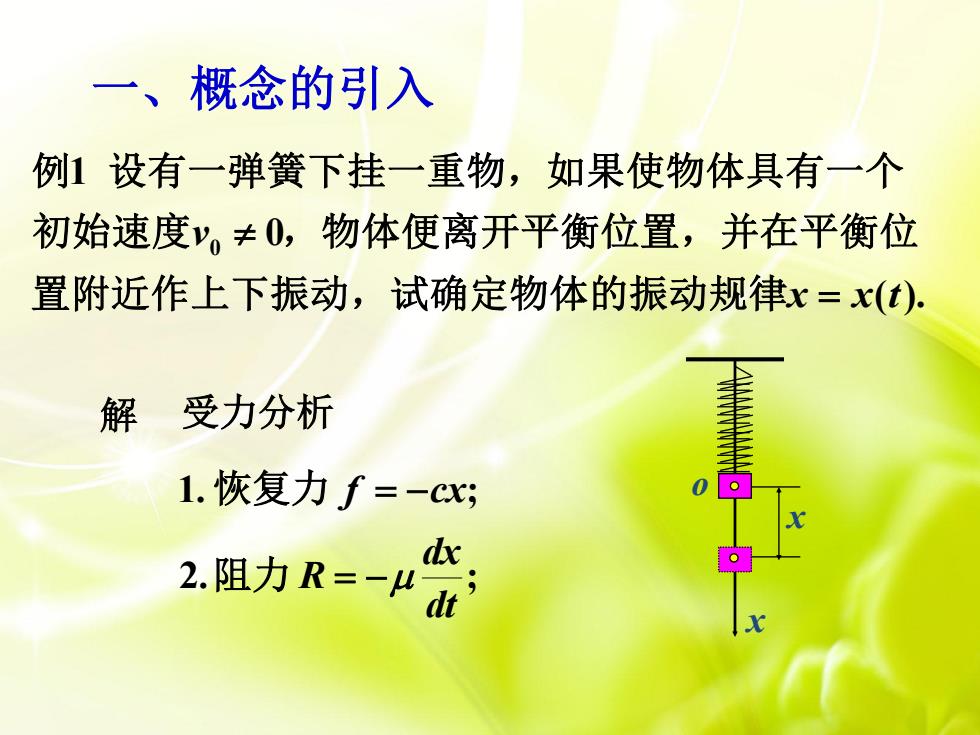
一、概念的引入例1设有一弹簧下挂一重物,如果使物体具有一个初始速度v。≠0,物体便离开平衡位置,并在平衡位置附近作上下振动,试确定物体的振动规律x=x(t)解受力分析1.恢复力f =-cx;.X一m·2.阻力R=-μx
解 受力分析 1.恢复力 f cx; 2. ; dt dx 阻力 R x x o 一、概念的引入 0 1 0 ( ). v x x t 例 设有一弹簧下挂一重物,如果使物体具有一个 初始速度 ,物体便离开平衡位置,并在平衡位 置附近作上下振动,试确定物体的振动规律

d'x一:F=ma, ..m=-cx-μdt?uC移项,并记2n =mmd'xdxkx=0物体自由振动的微分方程+2n+dtdt?若受到铅直干扰力F=Hsin pt,H得记hmd'x一2n强迫振动的方程+k'x = hsin pt+dt?
F ma, , 2 2 dt dx cx dt d x m 2 2 2 2 0 d x dx n k x dt dt 物体自由振动的微分方程 若受到铅直干扰力 F H sin pt, 2 2 2 2 sin d x dx n k x h pt dt dt 强迫振动的方程 2 2 , μ c n k m m 移项,并记 H h m 记 得
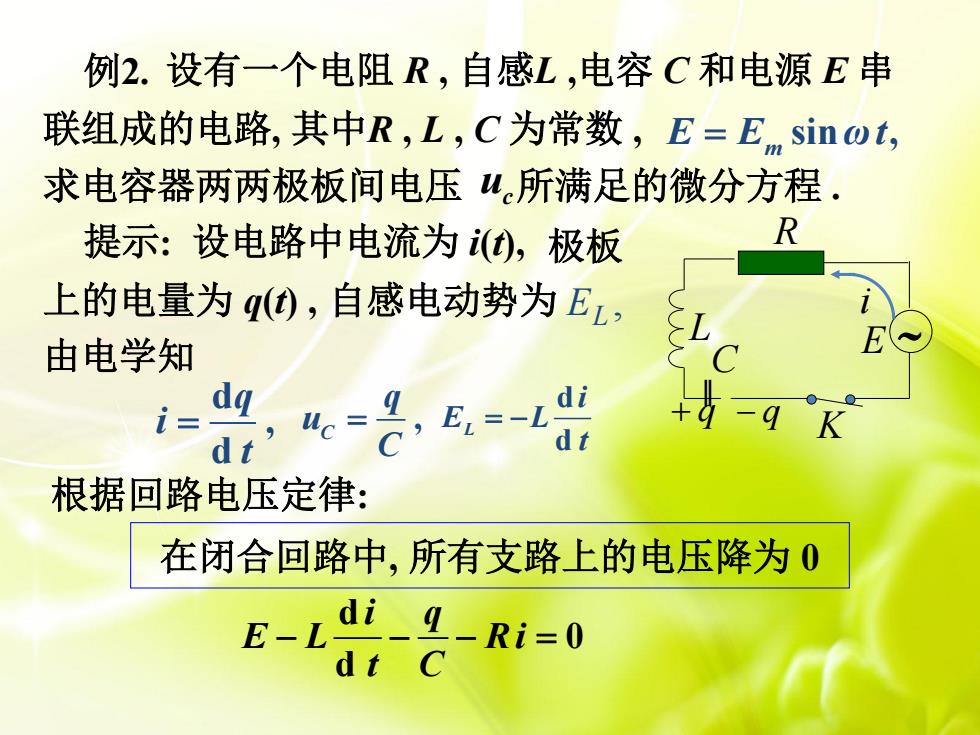
例2.设有一个电阻R,自感L,电容C和电源E串联组成的电路,其中R,L,C为常数,E=Esinのt,求电容器两两极板间电压u.所满足的微分方程,R提示:设电路中电流为i(t),极板上的电量为q(t),自感电动势为 ELE由电学知Cdidq.aX-q=E.=1Kdtdt根据回路电压定律:在闭合回路中,所有支路上的电压降为0diqE-LRi=0Cdt
求电容器两两极板间电压 d 0 d i q E L R i t C 例2. 联组成的电路, 其中R , L , C 为常数 , sin , E E m ωt uc 所满足的微分方程 . 提示: 设电路中电流为 i(t), ∼~ ‖ L E R K C q q 上的电量为 q(t) , 自感电动势为 , i EL 由电学知 d , d q i t , C q u C d d L i E L t 根据回路电压定律: 设有一个电阻 R , 自感L ,电容 C 和电源 E 串 极板 在闭合回路中, 所有支路上的电压降为 0

duc,故有化为关于u.的方程:注意i=Cdtd'ucduc +uc = E.sin otLC+RCdt?dtRR令β=02LLC人人LEC串联电路的振荡方程:+u-q Kd'ucEducm+2βsinot+0udt?LCdt如果电容器充电后撤去电源(E=0),则得d'ucduc +wiuc=0+2βdt?dt
0 1 , 2 R β ω L LC 令 2 2 2 0 d d 2 sin d d C C m C u u E β ω u ωt t t LC 串联电路的振荡方程: 如果电容器充电后撤去电源 ( E = 0 ) , 则得 2 2 2 0 d d 2 0 d d C C C u u β ω u t t ~ ‖ L E R K C q q i 2 2 d d sin d d C C C m u u LC RC u E ωt t t 化为关于 uc 的方程: d , d uC i C t 注意 故有