
第三节函数的极限一、 函数极限的定义二、 函数极限的性质三、小结 练习题
第三节 函数的极限 •一、函数极限的定义 •二、函数极限的性质 •三、小结 练习题

对 y=f(x),自变量变化过程的六种形式(1) x→xo(4)x-→8(2) x → xo(5)x→+80(6)x-→-8(3) x → xo本节内容:一、自变量趋于无穷大时函数的极限二、自变量趋于有限值时函数的极限
二、自变量趋于有限值时函数的极限 对 y f x ( ) , 0 0 0 (1) (2) (3) x x x x x x (4) (5) (6) x x x 自变量变化过程的六种形式: 一、自变量趋于无穷大时函数的极限 本节内容 :
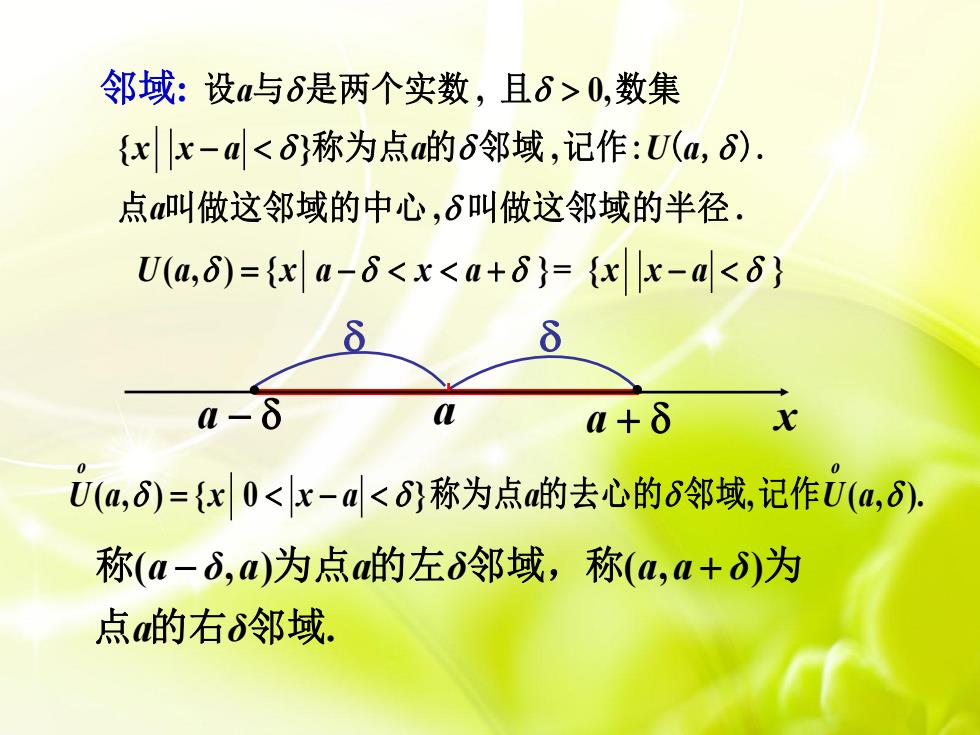
邻域:设a与8是两个实数,且>0,数集(xx-a<8})称为点a的8邻域,记作:U(a,s)。点a叫做这邻域的中心,叫做这邻域的半径U(a,8)=(xa-8<x<a+8)= (xx-a<8)88a-8aa+8xU(a,8)={x|0<|x-al<8)称为点a的去心的8邻域,记作U(a,8),称(a-,a)为点a的左邻域,称(a,a+)为点a的右邻域
邻域: , 0, { } , , . a x x a a U a a 设 与 是两个实数 且 数集 称为点 的 邻域 记作: ( , ). 点 叫做这邻域的中心 叫做这邻域的半径 U a x a x a x x a ( , ) { }= { } a a a x ( , ) { 0 } , ( , ). o o U a x x a a U a 称为点 的去心的 邻域 记作 ( , ) ( , ) . a δ a a δ a a δ a δ 称 为点 的左 邻域,称 为 点 的右 邻域

函数极限的定义一、1、自变量趋向有限值时函数的极限问题:函数y=f(x)在x→x,的过程中;对应函数值f(x)无限趋近于确定数Af(x)-A<ε 表示|f(x)-A任意小;0<x-x< 表示x→x,的过程SSxX-SX,+sXoS体现x接近x,程度
f x A f x A ( ) ( ) ; 表示 任意小 0 0 0 . x x x x 表示 的过程 x 0 x0 x 0 x 0 体现x x 接近 程度. 1、自变量趋向有限值时函数的极限 一、函数极限的定义 0 ( ) ( ) . y f x x x f x A 函数 在 的过程中, 对应函数值 无限趋 问 近于确定数 题:

定义1 设函数f(x)在x,的某个去心邻域内有定义,如果存在常数A,对于任意给定的正数ε(不论它有多么小,总存在正数8,使得当x满足不等式0<x-xl<S时,对应的函数值f(x)都满足不等式f(x)- A|<8,那么常数A就叫做函数f(x)当x→x,时的极限记作:lim f(x)= A 或 f(x)→A(当x→x,)x→Xo"&-8"定义>0,>0,使当0时恒有|f(x)-A<8
" "定 义 0 0, 0, 0 , ( ) . x x f x A 使当 时 恒有 0 0 0 0 0 ( ) ( ) 0 ( ) ( ) , ( ) lim ( ) ( ) 1 ( ) x x f x x A x x x f x f x A A f x x x f x A f x A x x 设函数 在 的某个去心邻域内有定义, 如果存在常数 ,对于任意给定的正数 不论它有 多么小 ,总存在正数 ,使得当 满足不等式 时,对应的函数值 都满足不等式 那么常数 就叫做函数 当 时的极限, 记作: 或 当 定义