
第六节 西数图形的描绘渐近线R二、 图形描绘的步骤三、作图举例四、小结
第六节 函数图形的描绘 • 一、渐近线 • 二、图形描绘的步骤 • 三、作图举例 • 四、小结

渐近线一、回顾:定义:当曲线 y=f(x)上的一动点P沿着曲线移向无穷点时,如果点P到某定直线L的距离趋向于零,那么直线L就称为曲线y=f(x)的一条渐近线1.铅直渐近线(垂直于x轴的渐近线)如果lim f(x) = 80 或 lim f(x)= 00x→xtx-→xo那么x=x,就是y=f(x)的一条铅直渐近线
定义: ( ) , , ( ) . y f x P P L L y f x = = 当曲线 上的一动点 沿着曲线 移向无穷点时 如果点 到某定直线 的距离 趋向于零 那么直线 就称为曲线 的 一条渐近线 1.铅直渐近线 ( ) 垂直于 x 轴的渐近线 0 0 0 lim ( ) lim ( ) ( ) . x x x x f x f x x x y f x → → + − = = = = 如果 或 那么 就是 的一条铅直渐近线 一、回顾:渐近线
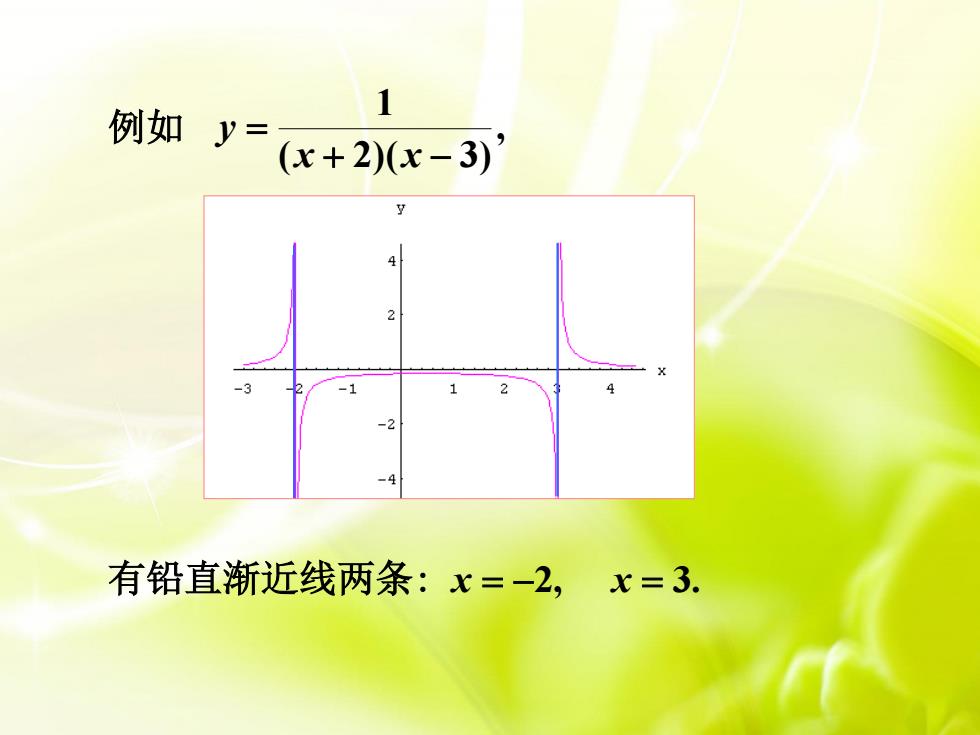
1例如y(x + 2)(x -3)212-2有铅直渐近线两条:x=-2,,x=3
例如 , ( 2)( 3) 1 + − = x x y 有铅直渐近线两条: x = −2, x = 3

(平行于x轴的渐近线)2.水平渐近线如果lim f(x)=c或 lim f(x)=c (c为常数)x→+00x→-80那么y=c就是y=f(x)的一条水平渐近线例如y=arctanx,0.51010-15-5515-0.1元元有水平渐近线两条:J=V=22
2.水平渐近线 ( ) 平行于 x 轴的渐近线 lim ( ) lim ( ) ( ) ( ) . x x f x c f x c c y c y f x →+ →− = = = = 如果 或 为常数 那么 就是 的一条水平渐近线 例如 y = arctan x, 有水平渐近线两条: . 2 , 2 = − y = y

3.斜渐近线如果lim [f(x)-(kx + b)]= 0x-→+或 lim[f(x)-(kx+b)]=0 (a,b为常数)x→-80那么y=kx+b就是y=f(x)的一条斜渐近线斜渐近线求法:f(x)lim[f(x)- kx] = b.lim=k,X-8x→00x那么y=kx+b就是曲线y=f(x)的一条斜渐近线
3.斜渐近线 lim [ ( ) ( )] 0 lim [ ( ) ( )] 0 ( , ) ( ) . x x f x kx b f x kx b a b y kx b y f x →+ →− − + = − + = = + = 如果 或 为常数 那么 就是 的一条斜渐近线 斜渐近线求法: ( ) lim , x f x k → x = lim[ ( ) ] . x f x kx b → − = 那么 y kx b y f x = + = 就是曲线 ( ) . 的一条斜渐近线