
第五节西数的微分问题的提出、微分的概念三、 可微的条件四、微分在近似计算中的应用五、微分在估计误差中的应用六、小结
第五节 函数的微分 • 一、问题的提出 • 二、微分的概念 • 三、可微的条件 • 四、微分在近似计算中的应用 • 五、微分在估计误差中的应用 • 六、小结
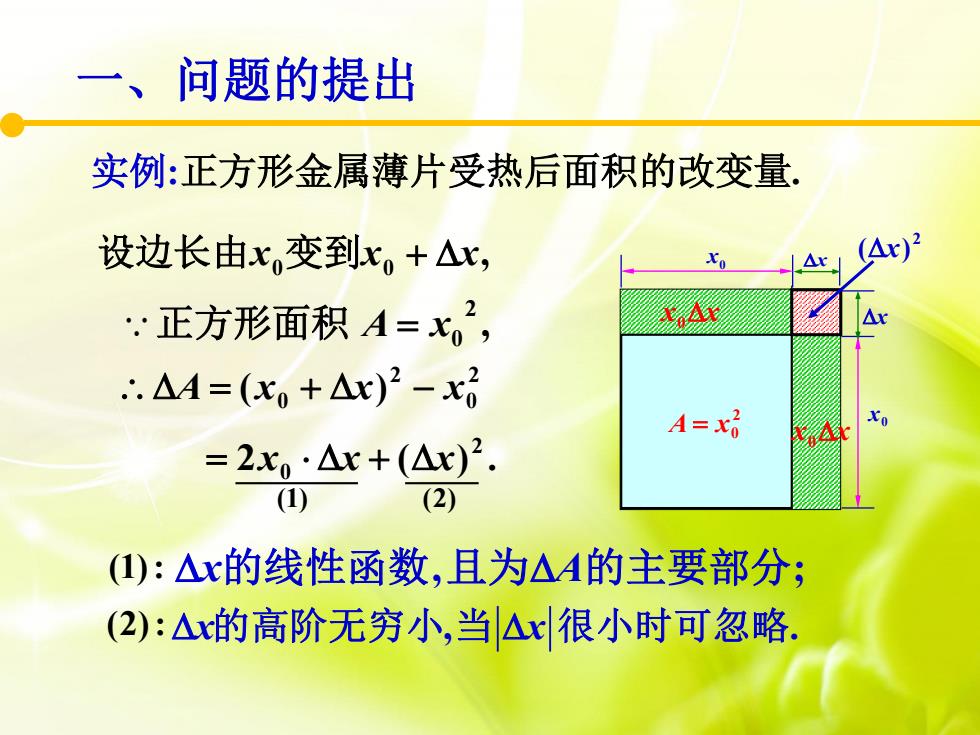
问题的提出实例:正方形金属薄片受热后面积的改变量(Ar)2设边长由x.变到x。+△x,AxLArAx:正方形面积A=x,.. A = (x, + Ax)2 - x)XoA=x:A= 2xo · Ax +(x)?(1)(2)(1):△x的线性函数,且为△A的主要部分:(2)△x的高阶无穷小,当△x很小时可忽略
实例:正方形金属薄片受热后面积的改变量. 2 A = x0 x0 0 x , 0 0 设边长由x 变到x + x , 2 0 正方形面积 A = x 2 0 2 0 A = (x + x) − x 2 ( ) . 2 = x0 x + x (1) (2) x的线性函数,且为A的主要部分; x x 的高阶无穷小, . 当 很小时可忽略 (1): (2): x x 2 (x) x x 0 x x 0 一、问题的提出

再例如,设函数y=x在点x.处的改变量为△x时,求函数的改变量△yAy =(x, + Ax)3 - x3= 3x .Ar +3x, ·(Ax) +(Ax)3(1)(2)当△x|很小时,(2)是△x的高阶无穷小o(△x),:. Ay ~ 3x? · Ax.既容易计算又是较好的近似值问题:这个线性函数(改变量的主要部分)是否所有函数的改变量都有?它是什么?如何求?
再例如, , . 0 3 x y y x x = 为 时 求函数的改变量 设函数 在点 处的改变量 3 0 3 0 y = (x + x) − x 3 3 ( ) ( ) . 2 3 0 2 = x0 x + x x + x (1) (2) 当 x 很小时, 3 . 2 y x0 x (2)是x的高阶无穷小o(x), 既容易计算又是较好的近似值 问题:这个线性函数(改变量的主要部分)是否 所有函数的改变量都有?它是什么?如何求?

二、微分的概念设函数y= f(x)在某区间内有定义1.定义x,及x。+△x在这区间内,如果Ay = f(x, + Ax)- f(x) = A· △x +o(△x)成立(其中A是与△x无关的常数),则称函数y=f(x)在点x,可微,并且称A·△x为函数y= f(x)在点x,相应于自变量增量△Ax的微分记作dy或df(x),即dy=A·Ax.微分dy叫做函数增量△y的线性主部(微分的实质)
1.定义0 0 0 0 0 0 ( ) , , ( ) ( ) ( ) ( ), ( ) , ( ) , ( ), . y f x x x x y f x x f x A x o x A x y f x x A x y f x x x dy df x dy A x = + = + − = + = = = 设函数 在某区间内有定义 及 在这区间内 如果 成立 其中 是与 无关的常数 则称函数 在点 可微 并且称 为函数 在点 相应于自变量增量 的微分 记作 或 即 微分dy叫做函数增量 y的线性主部. (微分的实质) 二、微分的概念

由定义知:(1)dy是自变量的改变量△r的线性函数;(2)Ay-dy=o(△x)是比△x高阶无穷小;(3)当A±0时,dy与△Ay是等价无穷小:Ay0(△x)→1 (△x →0)dyA.△r(线性主部);(4)当△x很小时,Ay~dy(5) A是与△x无关的常数,但与f(x)和x,有关
由定义知: ( ) ; 1 dy x 是自变量的改变量 的线性函数 ( ) ( ) ; 2 − = y dy o x x 是比 高阶无穷小 ( ) , ; 3 0 当A dy y 时 与 是等价无穷小 dy y A x o x = + ( ) 1 → 1 (x → 0). 0 ( ) , ( ) . 5 A x f x x 是与 无关的常数 但与 和 有关 (4) , ( ); 当 x y dy 很小时 线性主部