二、曲面的面积 ①.设曲面S的方程为: 在xOy面上的投影区域为D, 如图,设小区域do∈D, 取点P(x,y)∈do, 设S上点M(x,f(x,y)在 xOy面的投影是P, -P(x,y) do ∑为S上过M的切平面. 以do为准线,以平行于轴的直线为母线做柱面,柱面 与曲面S交与一小片曲面,与交与一小片平面
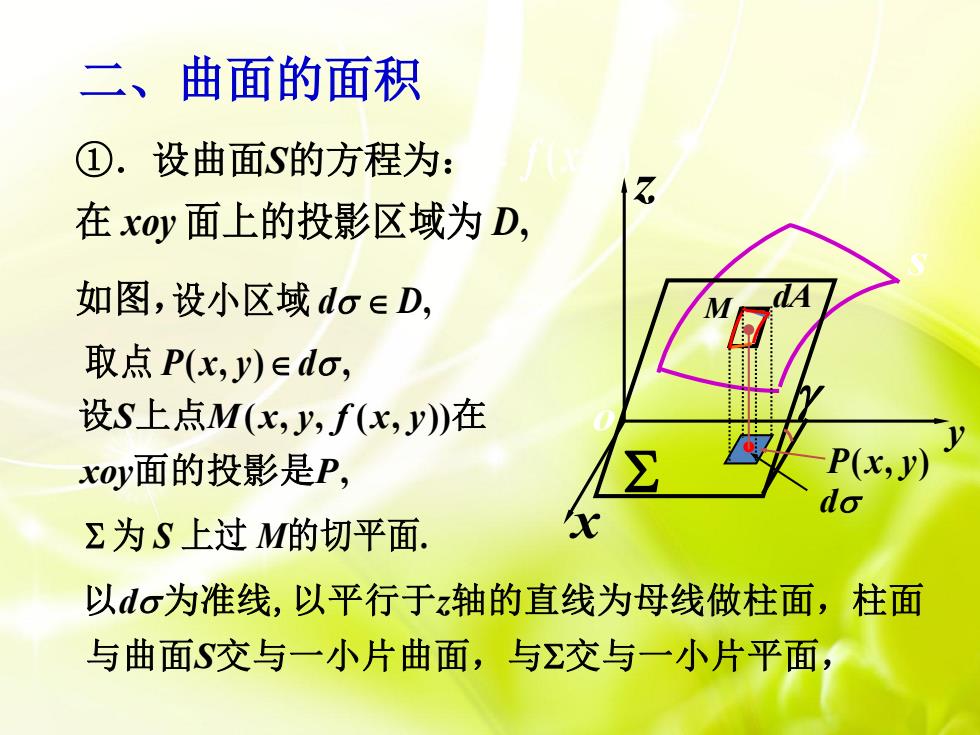
①.设曲面S的方程为: z f x y ( , ) 在 xoy D 面上的投影区域为 , 取点 P x y d ( , ) , 如图, 设小区域 d D , 为 S M 上过 的切平面. 二、曲面的面积 dP x y ( , ) M dA x y z s o ( , , ( , )) , S M x y f x y xoy P 设 上点 在 面的投影是 d z S 以 为准线,以平行于 轴的直线为母线做柱面,柱面 与曲面 交与一小片曲面,与 交与一小片平面

由于dσ很小,切平面Σ的小片平面面积A可以 代替相应的那小片曲面的面积. 设点M处曲面S上的法线(指向朝上)与z轴的 所成的角为y, .do为dA在xoy面上的投影, ∴.do=dA.cosy, 1 cosy= 1+f+f .dM=1+f经+fdo 曲面S的面积元素 以dσ为准线,以平行于z轴的直线为母线做柱面,柱面 与曲面交与一小片曲面,与交与一小片平面
曲面S的面积元素 由于d dA 很小,切平面的小片平面 积 可以 代替相应的那小片曲面的 积. M S z ( ) 设点 处曲面 上的法线 指向朝上 与 轴的 所成的角为 , d dA xoy 为 在 面上的投影, d dA cos , 2 2 1 cos , 1 x y f f 2 2 1 x y dA f f d d z S 以 为准线,以平行于 轴的直线为母线做柱面,柱面 与曲面 交与一小片曲面,与 交与一小片平面

同理可得 ②.设曲面的方程为:x=g(y,) 曲面面积公式为:A=J∬V1+g,2+g:2d; D ③.设曲面的方程为:y=h(亿,x) 曲面面积公式为:A=小V1+:2+hk水
②.设曲面的方程为: x g y z ( , ) 曲面面积公式为: 2 2 1 ; yz y z D A g g dydz ③.设曲面的方程为: y h z x ( , ) 曲面面积公式为: 2 2 1 . zx z x D A h h dzdx 同理可得

例2求球面x2+y2+z2=2含在圆柱体 x2+y2=c内部的那部分面积. 有对称性知A=44 解 D,:x2+Jy2≤x,(,y20) 曲面的方程为z=Va2-x2-y2 于*8- A=4∬V1+:2+z
解 2 2 1 D x y ax x y : , ( , 0) 曲面的方程为 2 2 2 2 2 2 2 . x y z a x y ax 例 求球面 含在圆柱体 内部的那部分面积 1 有对称性知A A 4 2 2 2 z a x y 2 2 2 2 2 1 , z z a x y a x y 于是 1 2 2 4 1 x y D A z z dxdy o x y z a

-dxdy =nieG云pr- 例3求半径为R的球面的表面积 解 曲面方程为z=√R2-x2-y A=8A,=8V1+2+ (由对称性) =4πR2
1 2 2 2 4 D a dxdy a x y 2 cos 0 0 2 2 1 4 a a d d a 2 2 2 4 . a a 求半径为R的球面的表面积 解 曲面方程为 (由对称性) 1 2 2 1 8 8 1 x y D A A z z dxdy 1 2 2 2 8 D R dxdy R x y 2 2 2 0 0 8 R R d d R 2 4 R 例3 2 2 2 z R x y