
第四节空间直孩及其方程 ·一、空间直孩的一般方程 ·二、空间直孩的对称式方程与参教方程 ·三、两直孩的夹角 ·四、直孩与平面的夹角 ·五、年面束 ·六、小结
第四节 空间直线及其方程 • 一、空间直线的一般方程 • 二、空间直线的对称式方程与参数方程 • 三、两直线的夹角 • 四、直线与平面的夹角 • 五、平面束 • 六、小结
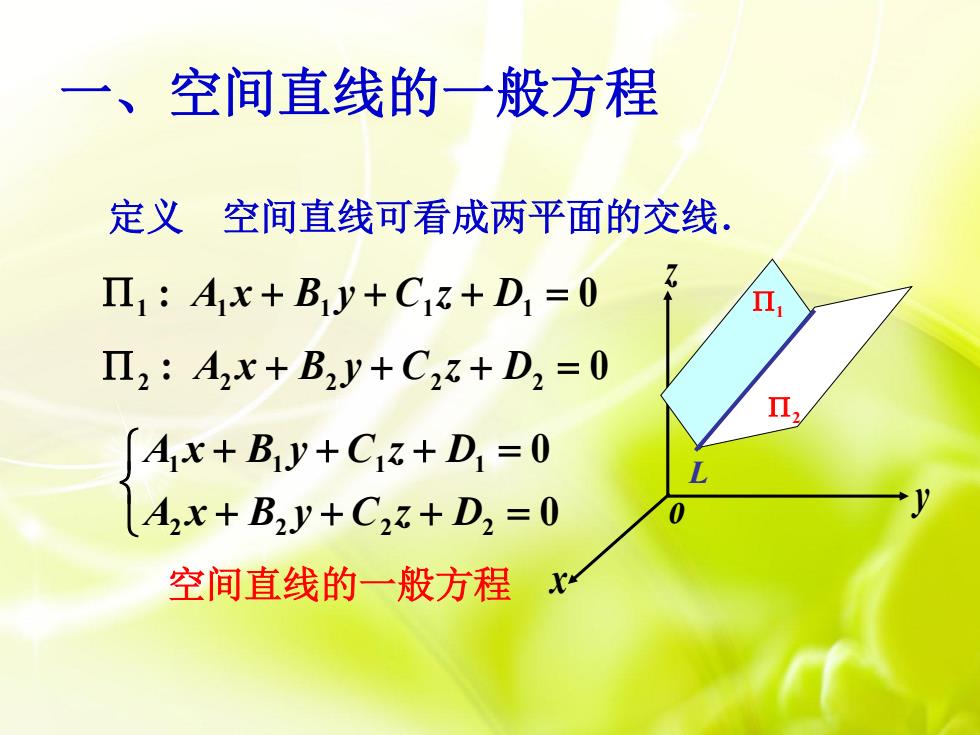
一、 空间直线的一般方程 定义空间直线可看成两平面的交线. Π1:Ax+By+C1z+D1=0 Π2:A2x+B2Jy+C2+D2=0 Ax+By+C+D=0 A2x+B2y+C27+D2=0 空间直线的一般方程x
x y z o 1 2 定义 空间直线可看成两平面的交线. : 0 1 A1 x B1 y C1z D1 : 0 2 A2 x B2 y C2 z D2 0 0 2 2 2 2 1 1 1 1 A x B y C z D A x B y C z D 空间直线的一般方程 L 一、空间直线的一般方程

二、空间直线的对称式方程与参数方程 方向向量的定义: 如果一非零向量平行于一 条已知直线,这个向量称为 这条直线的方向向量. 5={m,n,ph,Mo(xo,5o,zo), VM∈L,M(x,y,z), MoMI∥ MoM={x-xo,y-yo,-Z03
x y z o 方向向量的定义: 如果一非零向量平行于一 条已知直线,这个向量称为 这条直线的方向向量. s L ( , , ), 0 0 0 0 M x y z M0 M M L, M ( x, y,z), M M s 0 // s {m, n, p}, { , , } 0 0 0 0 M M x x y y z z 二、空间直线的对称式方程与参数方程
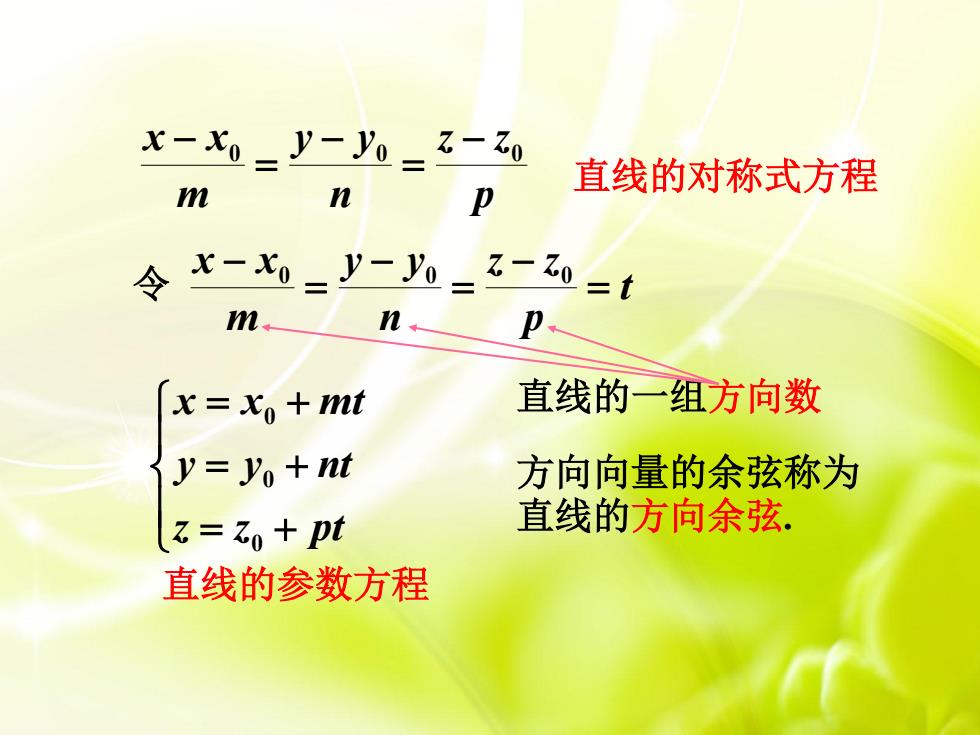
x-xoy-yo3-Z0 直线的对称式方程 n 令七-0=y-4=-0=t m. n. x=x+mt 直线的一组方向数 y=yo+nt 方向向量的余弦称为 Zo pt 直线的方向余弦, 直线的参数方程
p z z n y y m x x0 0 0 直线的对称式方程 t p z z n y y m x x 令 0 0 0 z z pt y y nt x x mt 0 0 0 直线的一组方向数 方向向量的余弦称为 直线的方向余弦. 直线的参数方程

例1用对称式方程及参数方程表示直线 x+y+z+1=0 2x-y+3z+4=0 解 在直线上任取一点(K,y,0) 取七,=1→+名,+2=0 y-3z0-6=0 解得y=0,z=-2 点坐标(1,0,-2)
例1 用对称式方程及参数方程表示直线 1 0 2 3 4 0 x y z x y z 解 在直线上任取一点 ( , , ) 0 0 0 x y z 取 1 x0 , 3 6 0 2 0 0 0 0 0 y z y z 解得 0, 2 y0 z0 点坐标 (1,0, 2)