
复变函数3收敛圆与收敛半径对于一个幂幕级数,其收敛半径的情况有三种(1)对所有的正实数都收敛.即级数在复平面内处处收敛(2)对所有的正实数除z=0 外都发散此时,级数在复平面内除原点外处处发散(3既存在使级数发散的正实数,也存在使级数收敛的正实数,u
11 (3) 既存在使级数发散的正实数, 也存在使级数收 敛的正实数. 此时, 级数在复平面内除原点外处处发散. 3)收敛圆与收敛半径 对于一个幂级数, 其收敛半径的情况有三种: (1)对所有的正实数都收敛.即级数在复平面内处 处收敛. (2) 对所有的正实数除 z = 0 外都发散
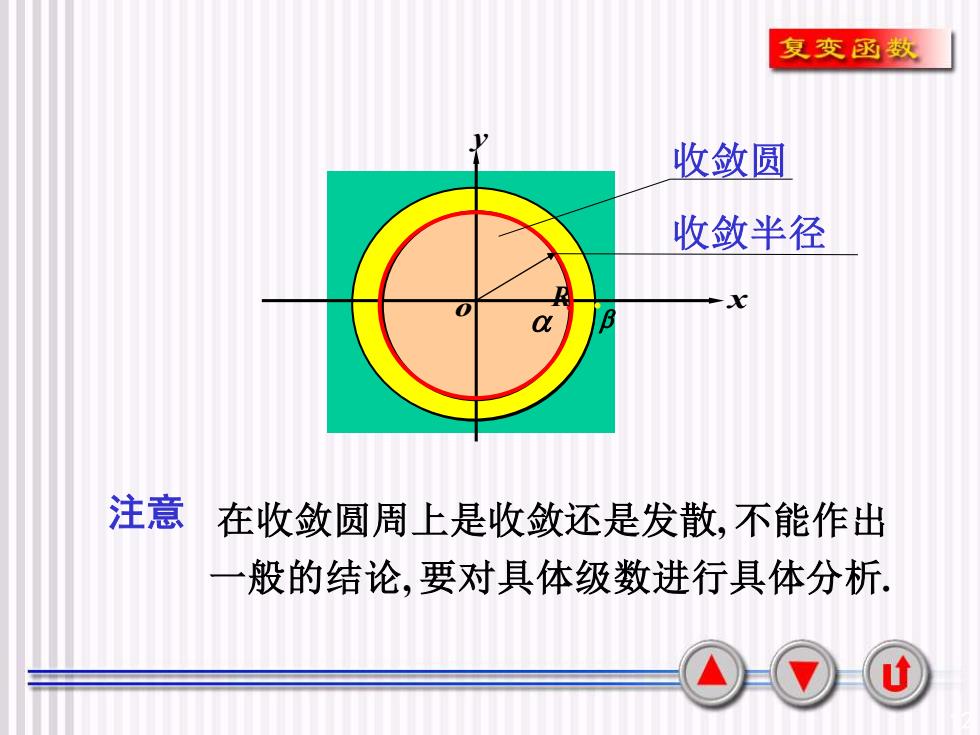
复变函数收敛圆收敛半径1x0Ba注意在收敛圆周上是收敛还是发散,不能作出一般的结论,要对具体级数进行具体分析U
12 在收敛圆周上是收敛还是发散, 不能作出 一般的结论, 要对具体级数进行具体分析. 注意 x y o . R. 收敛圆 收敛半径

复变函数4)收敛半径的求法方法1:比值法Cn+1如果=±0,Jlim那未收敛半径R=an-00Cn方法2:根值法如果 lim/cn=≠0,那末收敛半径 R-2n>1/2, 0<<+80;即2= 0;R=3 + 8,0,α = +8.u
13 方法1: 比值法 方法2: 根值法 4)收敛半径的求法 lim 0, 1 = + → n n n c c 如果 那末收敛半径 . 1 R = = + + = + = 0, . , 0; 1 , 0 ; 即 R lim = 0, → n n n 如果 c 那末收敛半径 . 1 R =

复变函数5)幂级数的运算与性质c8(I)设 f(z)=a,z", R=ri, g(z)=)Mb,z", R= r2n=0n=0888Zbhz" =(an ±bn)z",土f(z)±g(z) =nzann=0n=0n=088R=min(r,r2)f(z): g(z)=(anz").(bnz"),n=0n=08Z(a,b +an-ib ++aob,)z",<Rn=0U
14 (1) ( ) , , ( ) , . 2 0 1 0 f z a z R r g z b z R r n n n n n = n = = = = = 设 ( ) ( ) ( ) , 0 0 0 n n n n n n n n n n f z g z = a z b z = a b z = = = ( ) ( ) ( ) ( ), 0 0 = = = n n n n n n f z g z a z b z = = + − + + 0 0 1 1 0 ( ) , n n n n n a b a b a b z z R min( , ) 1 2 R = r r 5)幂级数的运算与性质

复变函数(2)幂级数的代换(复合)运算8-Z如果当 z<r 时,f(z)=anz",又设在n=0z<R 内 g(z)解析且满足g(z)<r,那末当z<RO时, f[g(z) =an[g(z)".n=0复变幂级数在收敛圆内的解析性c,(z-zo”的收敛半径为R,那末设幂级数n=0(l)它的和函数 f(z),即 (z)=cn(z一zo)"n=0是收敛圆za<R内的解析函数u
15 如果当 z r 时, ( ) , 0 = = n n n f z a z 又设在 z R 内 g(z) 解析且满足 g(z) r, 那末当 z R 时, = = 0 [ ( )] [ ( )] . n n n f g z a g z (2)幂级数的代换(复合)运算 复变幂级数在收敛圆内的解析性 = − 0 0 ( ) n n n 设幂级数 c z z 的收敛半径为 R, 那末 是收敛圆 z − a R 内的解析函数 . 它的和函数 = = − 0 0 ( ) ( ) n n n (1) f (z) , 即 f z c z z