
复变函数第五章留数一、重点与难点二、 内容提要三、典型例题U

复变函数一、重点与难点重点:留数的计算与留数定理难点:留数定理在定积分计算上的应用
2 一、重点与难点 重点: 难点: 留数的计算与留数定理 留数定理在定积分计算上的应用
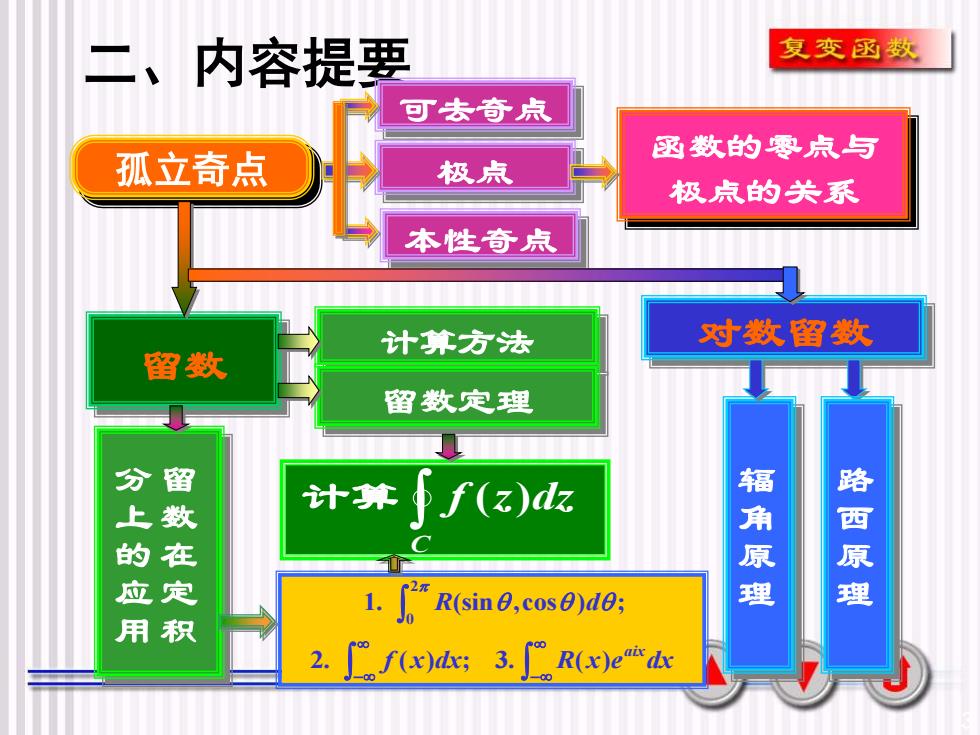
复变函数二、内容提要可去奇点函数的零点与孤立奇点极点极点的关系本性奇点对数留数计算方法留数留数定理分上的应用留数在定路西原理辐角原理f(z)dz计算R(sine,cos)de;积R(x)e*dxf(x)dx; 3
3 二、内容提要 留数 计算方法 可去奇点 孤立奇点 极点 本性奇点 函数的零点与 极点的关系 对数留数 留数定理 留 数 在 定 积 分 上 的 应 用 C 计算 f (z)dz − − f x dx R x e dx R d aix 2. ( ) ; 3. ( ) 1. (sin ,cos ) ; 2 0 辐 角 原 理 路 西 原 理

复变函数1.孤立奇点的概念与分类1)定义 如果函数f(z)在z不解析,但 f(z)在 Zo的某一去心邻域0<z一zo<内处处解析,则称zo 为f(z)的孤立奇点孤立奇点一奇点2)孤立奇点的分类依据()在其孤立奇点的去心邻域0<z-Zol< 内的洛朗级数的情况分为三类i)可去奇点;i)极点;ii)本性奇点U
4 1)定义 如果函数 f (z) 0 在 z 不解析, 但 f (z) 在 0 z 的某一去心邻域 − 0 0 z z 内处处解析, 则称 0 z 为 f (z) 的孤立奇点. 1. 孤立奇点的概念与分类 孤立奇点 奇点 2)孤立奇点的分类 依据 f (z) 在其孤立奇点 0 z 的去心邻域 − 0 0 z z 内的洛朗级数的情况分为三类: i) 可去奇点; ii) 极点; iii) 本性奇点

复变函数i)可去奇点定义如果洛朗级数中不含Z一Zo的负幂项,那末孤立奇点Z称为f(z)的可去奇点可去奇点的判定(a)由定义判断:如果f(z)在z。的洛朗级数无负幕项则z.为()的可去奇点(b)判断极限lim f(z):若极限存在且为有限值Z>z0则z为()的可去奇点U
5 定义 如果洛朗级数中不含 z − z0 的负幂项, 那末 0 孤立奇点 z 称为 f (z) 的可去奇点. i) 可去奇点