
复变函数第三节唯一决定分式线性映射的条件分式线性映射的确定一、二、分式线性映射对圆域的映射三、典型例题四、小结与思考U
第三节 唯一决定分式线性映射 的条件 一、分式线性映射的确定 二、分式线性映射对圆域的映射 三、典型例题 四、小结与思考

复变函数一、分式线性映射的确定az + b分式线性映射W=(ad-bc±0)cz + d含有三个独立的常数只需给定三个条件就能决定一个分式线性映射定理在z平面上任意给定三个相异的点z1,z2,73在w平面上也任意给定三个相异的点Wi,W2,W3那末就存在唯一的分式线性映射,将zk(k =1,2,3)依次映射成wk(k=1,2,3)u
2 一、分式线性映射的确定 含有三个独立的常数, ( − 0) + + = ad bc cz d az b 分式线性映射 w 定理 w (k = 1,2,3). 依次映射成 k , , , 1 2 3 在z平面上任意给定三个相异的点z z z , , , 在w平面上也任意给定三个相异的点w1 w2 w3 z (k = 1,2,3) 将 k 那末就存在唯一的分式线性映射, 只需给定三个条件就能决定一个分式线性映射

复变函数az + b证设W=(ad 一bc≠0)将相异点cz + dazk + b(k = 1,2,3)z(k = 1,2,3)依次映射成 Wk =Czk + d(z zk)(ad - bc)所以W-Wk(k = 1,2)(cz + d)(czk + d)(z3 - z)(ad - bc)(k = 1,2)W3Wk一(Cz3 + d)(Czk + d)Z3 - Z1Z - Z1w-wW33 -Wi由此得Z - Z2W- W27.3W3-W2-72U
3 所以w − wk w3 − wk 证 依次映射成 ( = 1,2,3) + + = k cz d az b w k k k z (k = 1,2,3) k ( − 0) + + = ad bc cz d az b 设 w 将相异点 由此得 3 2 3 1 2 1 : w w w w w w w w − − − − , ( 1,2) ( )( ) ( )( ) = + + − − = k cz d cz d z z ad bc k k , ( 1,2) ( )( ) ( )( ) 3 3 = + + − − = k cz d cz d z z ad bc k k : . 3 2 3 1 2 1 z z z z z z z z − − − − =

复变函数唯一性:az + b如果另一映射(ad 一bc≠ 0)也将W=cz + dazk +bzk (k=1,2,3)依次映射成 wk =(k = 1,2,3)czk + d重复上述步骤,仍得到相同形式的结果所以三对对应点可唯一确定一个分式线性映射[证毕]1
4 所以三对对应点可唯一确定一个分式线性映射. 唯一性: 如果另一映射 ( − 0)也将 + + = ad bc cz d az b w ( 1,2,3) ( = 1,2,3) + + = = k cz d az b z k w k k k 依次映射成 k 重复上述步骤, 仍得到相同形式的结果. [证毕]
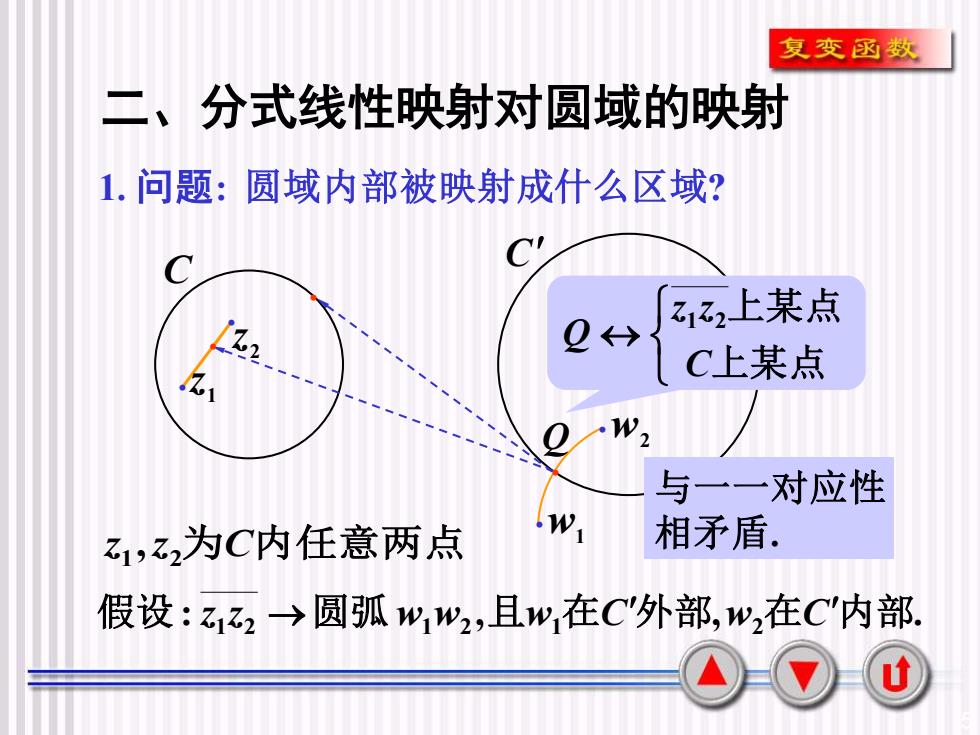
复变函数二、分式线性映射对圆域的映射1.问题:圆域内部被映射成什么区域?C'CZ2上某点0H5C上某点5wQ2与一一对应性.W相矛盾。Z1,Z2为C内任意两点假设:zz →圆弧 w,w2,且w,在C"外部,w,在C"内部U
5 二、分式线性映射对圆域的映射 1. 问题: 圆域内部被映射成什么区域? C C . . , z1 z2为C内任意两点 1 .z 2 z . w1 w2 . . . Q : , , . 假设 z1 z2 →圆弧 w1w2 且w1在C外部 w2在C内部 上某点 上某点 C z z Q 1 2 与一一对应性 相矛盾