
复变函数第二节分式线性映射一、分式线性映射的概念二、几种简单的分式线性映射三、分式线性映射的性质四、小结与思考u
第二节 分式线性映射 一、分式线性映射的概念 二、几种简单的分式线性映射 三、分式线性映射的性质 四、小结与思考

复变函数一、分式线性映射的概念az + b(ad -bc ±0,a,b,C,d均为常数.)w=cz + d称为分式线性映射小知识说明:1)ad一bc≠0的限制,保证了映射的保角性dwad -bc=0,有W=常数否则,由7dz(cz + d)那末整个平面映射成w平面上的一点U
2 一、分式线性映射的概念 (ad bc 0, a,b,c,d均为常数.) cz d az b w − + + = 称为分式线性映射. 说明: 否则, 由于 0, . d ( ) d 2 = 有 常数 + − = w cz d ad bc z w 那末整个z平面映射成 w平面上的一点. 1) ad − bc 0的限制,保证了映射的保角性. 小知识

复变函数az + b2) 由w=(ad -bc ± 0)cz + ddw+b(ad-bc±0Z:cw-a分式线性映射的逆映射.也是分式线性映射α+β三3)两分式线性映射 W(αs-β±0)ys+α'z + β(αs"-β0)仍复合为分式线性映Cyz+s"az + b射W二(ad -bc = (αs - βy)(α's"-β'r) ± 0)cz + dU
3 分式线性映射的逆映射, 也是分式线性映射. 2) 由 ( − 0) + + = ad bc cz d az b w ( − 0) − − + = ad bc cw a dw b z 3) 两分式线性映射 ( − 0) + + = w ( − 0) + + = z z 仍复合为分式线性映 (( − = ( − )( − ) 0)) + + = ad bc cz d az b 射 w

复变函数4)分式线性映射α+βasα1β-W=+Y+S0+sY令51= 5 +8,52则w = A5, + B(A,B为常数)2=7S一个一般形式的分式线性映射是由下列三种特殊的简单映射复合而成:(3) w=(1) w= z+ b,(2) w = az,Zα+β对w=的研究可化为对以上映射的研究ys+s1
4 4) 分式线性映射 + + = − + + = 1 w , 1 , 1 1 2 令 = + = 一个一般形式的分式线性映射是由下列三种 特殊的简单映射复合而成: (1) w = z + b, 对 的研究可化为对以上映射的研究. + + w = ( , ) 则w = A 2 + B A B为常数 (2) w = az, . 1 (3) z w =
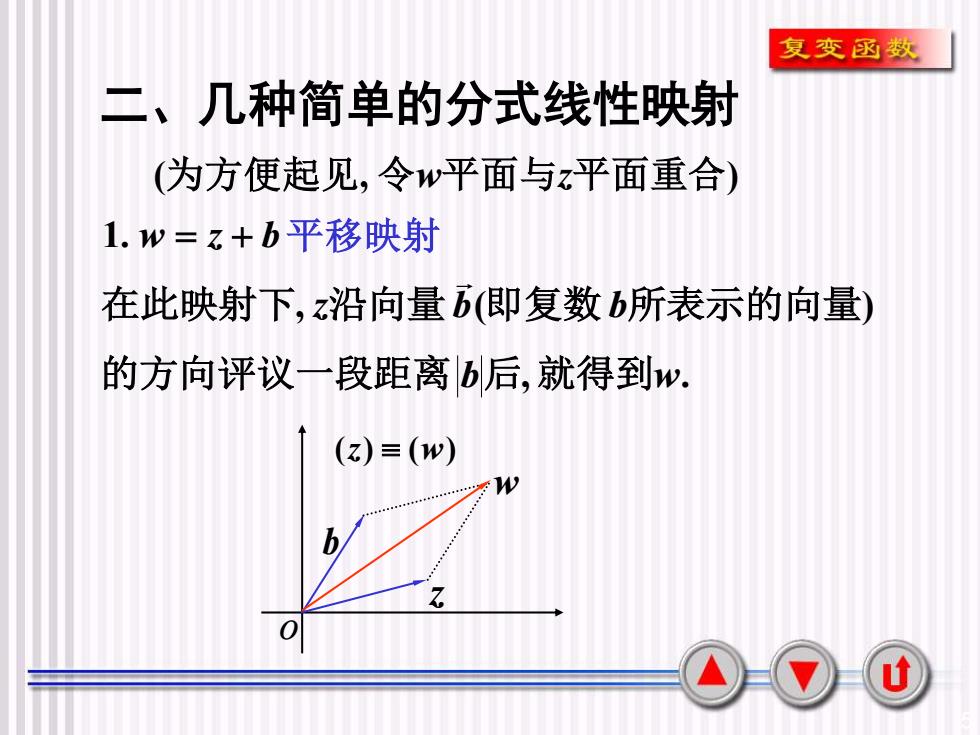
复变函数二、几种简单的分式线性映射(为方便起见,令w平面与z平面重合)1.w=z+b平移映射在此映射下,z沿向量b(即复数b所表示的向量)的方向评议一段距离b后,就得到W(z)= (w)W70u
5 二、几种简单的分式线性映射 1. w = z + b 平移映射 (为方便起见, 令w平面与z平面重合) 在此映射下, z沿向量b(即复数b所表示的向量) 的方向评议一段距离 b后,就得到w. o (z) (w) z b w