
复变函数第四节 原函数与不定积分一、主要定理和定义二、典型例题三、小结与思考u
第四节 原函数与不定积分 一、主要定理和定义 二、典型例题 三、小结与思考

复变函数主要定理和定义、E1.两个主要定理:定理一如果函数 f(z)在单连通域B内处处解析那末积分((z)dz与连结起点及终点的路线C无关.由定理一可知:解析函数在单连通域内的积分只与起点和终点有关,(如下页图)u
2 一、主要定理和定义 定理一 . ( )d ( ) , 无 关 那末积分 与连结起点及终点的路线 如果函数 在单连通域 内处处解析 C f z z f z B C 由定理一可知: 解析函数在单连通域内的积分只与起点 和终点有关, (如下页图) 1. 两个主要定理:
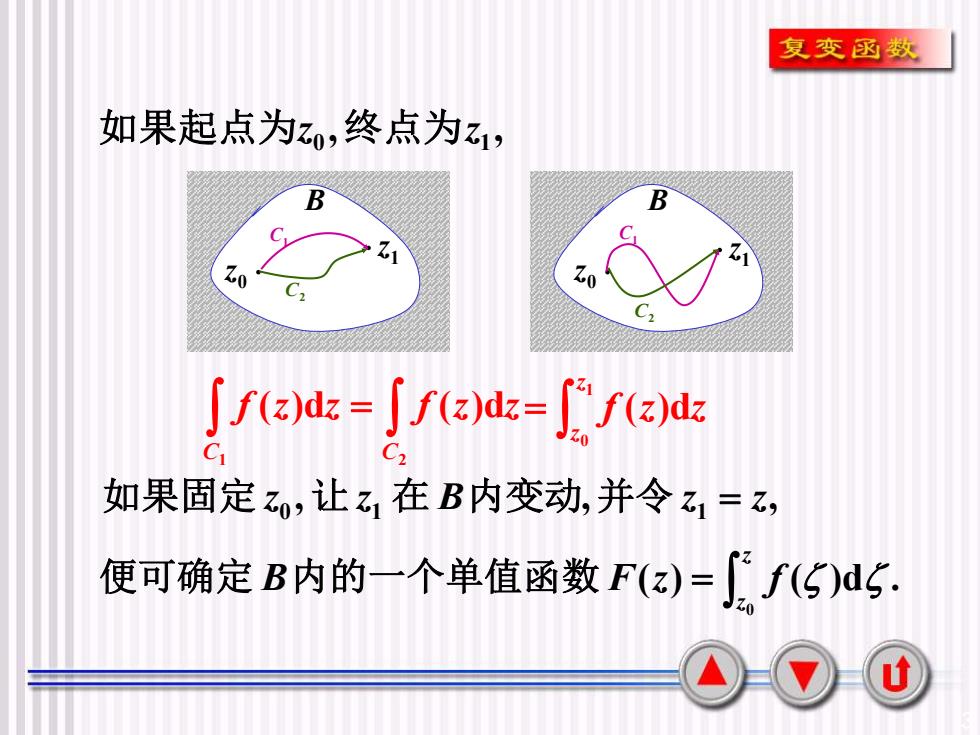
复变函数如果起点为Z,终点为zBBZ1Z1Zo10C2C2[ f(z)dz =J f(z)dz=(f(z)dz70如果固定 zo,让z 在 B内变动,并令 z= Z,便可确定 B内的一个单值函数 F(z)=(f(S)du
3 B B 0 z 1 z 0 z 1 z C1 C2 C1 C2 , , 0 1 如果起点为z 终点为z = 1 2 ( )d ( )d C C f z z f z z = 1 0 ( )d z z f z z , , , 0 1 1 如果固定 z 让 z 在 B内变动 并令 z = z ( ) ( )d . 0 = z z 便可确定 B内的一个单值函数 F z f
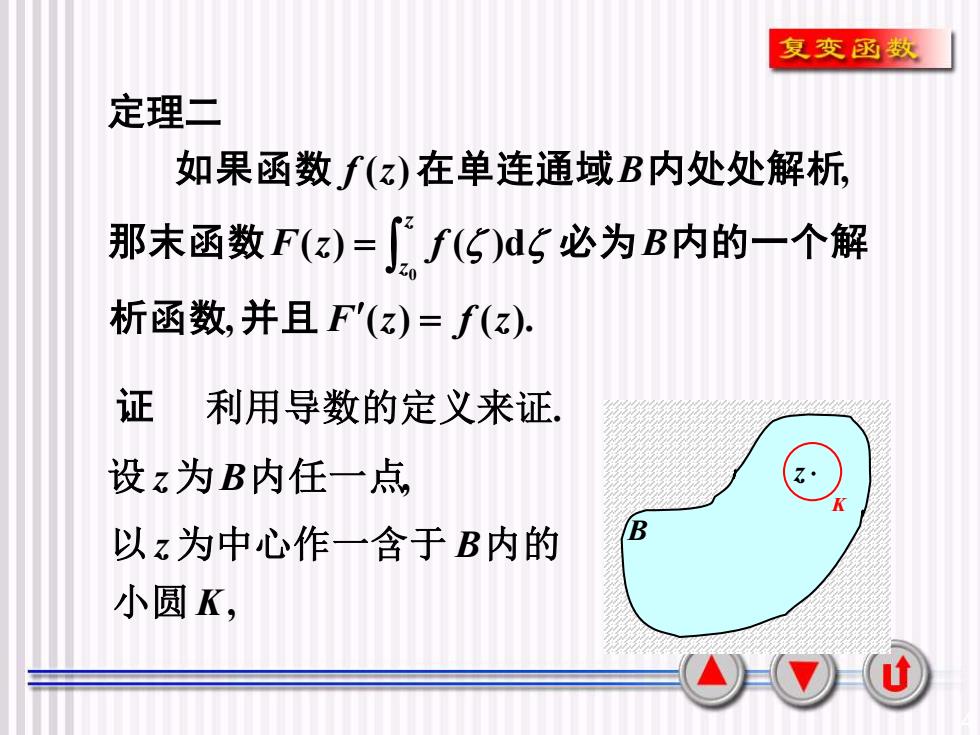
复变函数定理二如果函数 f(z)在单连通域B内处处解析那末函数F(z)=()d必为B内的一个解析函数,并且F(z)= f(z)证利用导数的定义来证。设z为B内任一点7KB以z为中心作一含于B内的小圆K,u
4 , ( ) ( ). ( ) ( )d ( ) , 0 F z f z F z f B f z B z z = = 析函数 并 且 那末函数 必 为 内的一个解 如果函数 在单连通域 内处处解析 定理二 证 利用导数的定义来证. B 设 z为B内任一点, z , K z B 小圆 以 为中心作一含于 内的 K
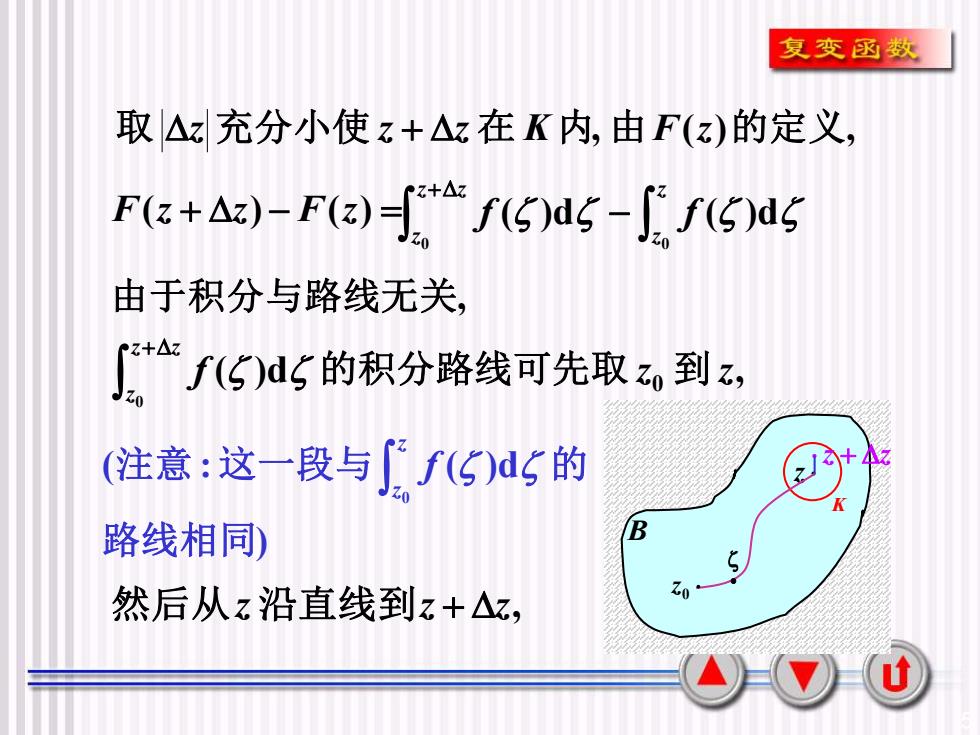
复变函数取△z充分小使z +△z在K内, 由 F(z)的定义Z+AZf(S)ds -"f(S)dsF(z+ △z) - F(z) =(7由于积分与路线无关Cz+Azf(S)d的积分路线可先取Z到z,JZo2+4z(注意:这一段与f()ds的20KB路线相同)SZo然后从z沿直线到z+△z,u
5 B z K 取 z 充分小使 z + z 在 K内, z + z F(z + z) − F(z) = − + z z z z z f f 0 0 ( )d ( )d 由于积分与路线无关, ( )d , 0 0 f z z z z z 的积分路线可先取 到 + 然后从z 沿直线到z + z, 0 z • ) ( : ( )d 0 路线相同 注意 这一段与 的 z z f 由F(z)的定义