
复变函数*第四节平面场的复势一、用复变函数表示平面向量场二、平面流速场的复势三、静电场的复势四、小结与思考U
*第四节 平面场的复势 一、用复变函数表示平面向量场 二、平面流速场的复势 三、静电场的复势 四、小结与思考
复变函数一、用复变函数表示平面向量场平面定常向量场向量场中的向量都平行于某一个平面S.而且在垂直于S的任何一条直线上的所有点处的向量都是相等的:场中的向量也都与时间无关显然,向量场在所有平行于S的平面内的分布情况是完全相同的.可以用S。平面内的场表示U
2 一、用复变函数表示平面向量场 平面定常向量场: 向量场中的向量都平 行于某一个平面S, 而且在 垂直于S 的任何一条直线 上的所有点处的向量都是 相等的; 场中的向量也都与 时间无关. S S0 显然, 向量场在所有平行于S 的平面内的分布情 况是完全相同的, 可以用So 平面内的场表示

复变函数在平面S.内取定一直角坐标系xoy向量A=Ai+A可表示为复数A=Ax+iA由于场中的点可用复数z=x+i表示所以平面向量场 A=Ax(x,J)i +A,(x,J)j可表示为复变函数 A= A(z)= Ax(x,J)+iA,(x,y)反之,已知一个复变函数w=u(x,y)+iv(x,y),也可作出对应的平面向量场 A=u(x,y)i+v(x,y)iu
3 , 在平面S0内取定一直角坐标系xoy o x y Ay A . Ax x y x y A A iA A A i A j = + = + 为复数 向量 可表示 由于场中的点可用复数 z = x + iy 表示, ( ) ( , ) ( , ). ( , ) ( , ) A A z A x y iA x y A A x y i A x y j x y x y = = + = + 示为复变函数 所以平面向量场 可表 ( , ) ( , ) . , ( , ) ( , ), A u x y i v x y j w u x y iv x y = + = + 可作出对应的平面向量场 反之 已知一个复变函数 也

复变函数例如,一个平面定常流速场(如河水的表面)= vx(x,y)i +v,(x,y)j可以用复变函数=v(z)=V(x,J)+iv,(x,y)表示平面电场强度向量为E=Ex(x,y)i+E,(x,J))可以用复变函数E=E(z)=E(x,J)+,(x,J)表示
4 例如, 一个平面定常流速场(如河水的表面) v v x y i v x y j x y = ( , ) + ( , ) 可以用复变函数v v(z) v (x, y) iv (x, y)表示, = = x + y 平面电场强度向量为 E E x y i E x y j x y = ( , ) + ( , ) . ( ) ( , ) ( , ) 表示 可以用复变函数 E E z E x y iE x y = = x + y
复变函数二、平面流速场的复势1.流函数:设向量场讠是不可压缩的定常的理想流体的流速场:=yx(x,y)i +v,(x,y)j其中速度分量Vx(x,J)与v,(x,J)都有连续偏导数如果它在单连域B内是无源场(即管量场)OvOvOvavx即tX那末 div =:0.二dyaxayaxU
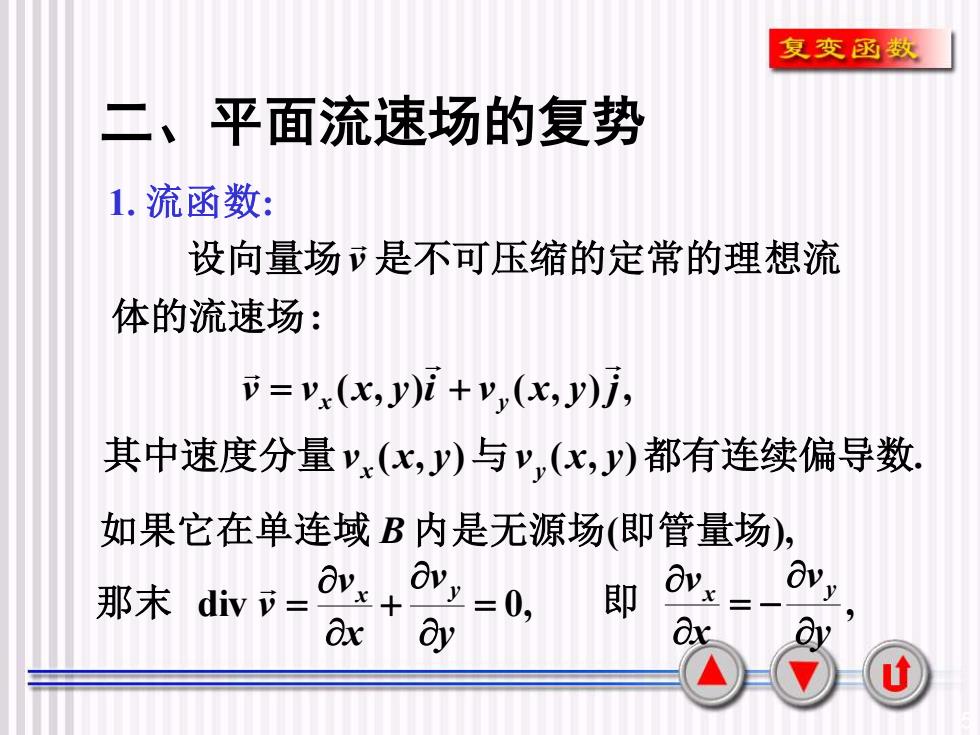
5 二、平面流速场的复势 1. 流函数: : 体的流速场 设向量场v 是不可压缩的定常的理想流 v v (x, y)i v (x, y) j, x y = + 其中速度分量v (x, y)与v (x, y)都有连续偏导数. x y 如果它在单连域 B 内是无源场(即管量场), div = 0, + = y v x v v 那末 x y , y v x vx y = − 即