《复变函数与积分变换》课程教学资源（PPT课件）第二章 解析函数 2.1 第一节 解析函数的概念

复变函数第一节解析函数的概念复变函数的导数与微分一、二、角解析函数的概念三、小结与思考U

第一节 解析函数的概念 一、复变函数的导数与微分 二、解析函数的概念 三、小结与思考

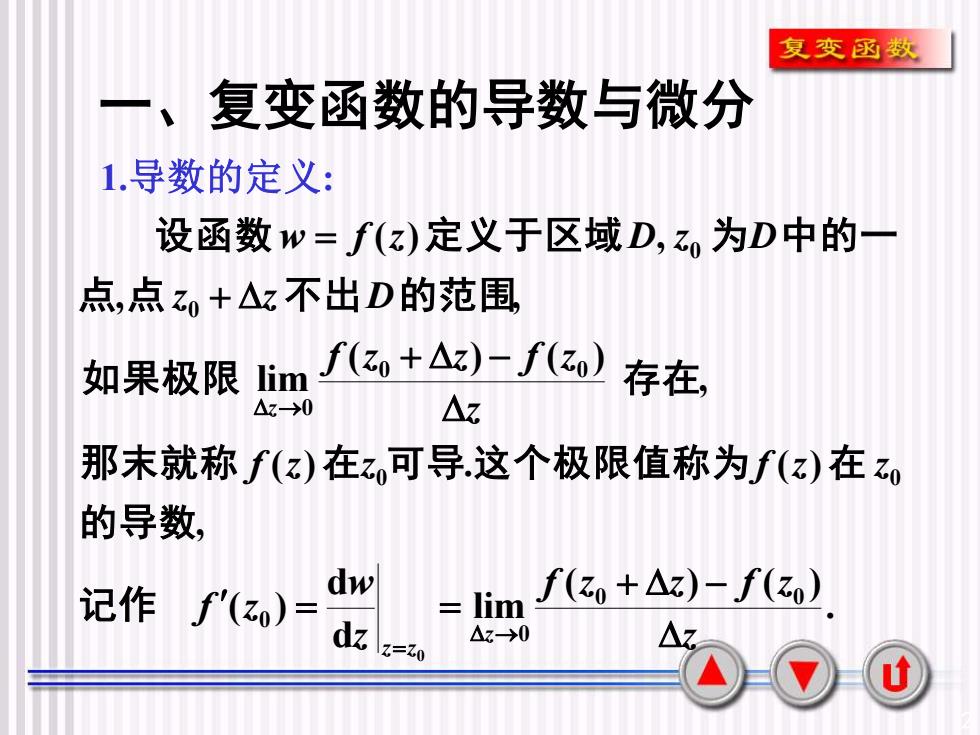
复变函数一、复变函数的导数与微分1.导数的定义：设函数w= f(z)定义于区域D,Zo为D中的一点,点Z+△z不出D的范围f(zo +△z)- f(zo)lim存在,如果极限AzAz-→0那末就称f(z)在z可导.这个极限值称为f(z)在zo的导数,dwf(zo +△z) - f(zo)记作limf'(zo)二Az.dzAz->0IZ=Z0U

2 一、复变函数的导数与微分 1.导数的定义: , , ( ) , 0 0 点 点 不 出 的范围 设函数 定义于区域 为 中的一 z z D w f z D z D +  = , ( ) . ( ) 0 0 的导数 那末就称 f z 在z 可 导 这个极限值称为f z 在 z . ( ) ( ) lim d d ( ) 0 0 0 0 0 z f z z f z z w f z z z z  +  −  = =  → = 记 作 , ( ) ( ) lim 0 0 0 如果极限 存 在 z f z z f z z  +  −  →

复变函数在定义中应注意：zoz→z(即→O)的方式是任意的即zo+△z在区域D内以任意方式趋于z时f(zo + △z) - f(zo)比值都趋于同一个数Az如果函数(z）在区域D内处处可导，我们就称f（z）在区域内D可导u

3 在定义中应注意: ( 0) . z0 + z → z0 即z → 的方式是任意的. ( ) ( ) , 0 0 0 0 比值 都趋于同一个数 即 在区域 内以任意方式趋于 时 z f z z f z z z D z  +  − +  ( ) . ( ) , 就 称 在区域内 可 导 如果函数 在区域 内处处可导 我 们 f z D f z D

复变函数例1 求f(z)=z"的导数f(z+z)- f(z)解f'(z) = limAzAz->0(z + z)2 - z2lim二AzAz-→>0lim(2z + Az) = 2z.=Az-→0(2) =2zu

4 例1 ( ) . 求f z = z2的导数 z f z z f z f z z  +  −  =  → ( ) ( ) ( ) lim0 解 z z z z z  +  − =  → 2 2 0 ( ) limlim ( 2 ) 0 z z z = +   → = 2 z . ( z ) 2 z 2 = 

复变函数例2讨论f(z)=Imz的可导性f -f(z+z)-f(z)Im(z + △z) - Im z解AzAzAzIm △zIm z + Im Az - Im zAzAzAyIm(Ax + iAy)Ax + iyAx + iAy当点沿平行于实轴的方向(△y=0)而使△z→0时，u

5 例2 讨论f (z) =Im z的可导性. z f z z f z zf  +  − =  ( ) ( ) 解 z z z z  +  − = Im( ) Im z z z z  +  − = Im Im Im z z  = Im x i y x i y  +   +  = Im( ) , x i y y  +   = 当点沿平行于实轴的方向(y = 0)而使z → 0时