
复变函数第三章复变函数的积分一、重点与难点二、 内容提要三、典型例题U

复变函数一、重点与难点重点:1.复积分的基本定理;2.柯西积分公式与高阶导数公式难点:复合闭路定理与复积分的计算拉
2 一、重点与难点 重点: 难点: 1. 复积分的基本定理; 2. 柯西积分公式与高阶导数公式 复合闭路定理与复积分的计算
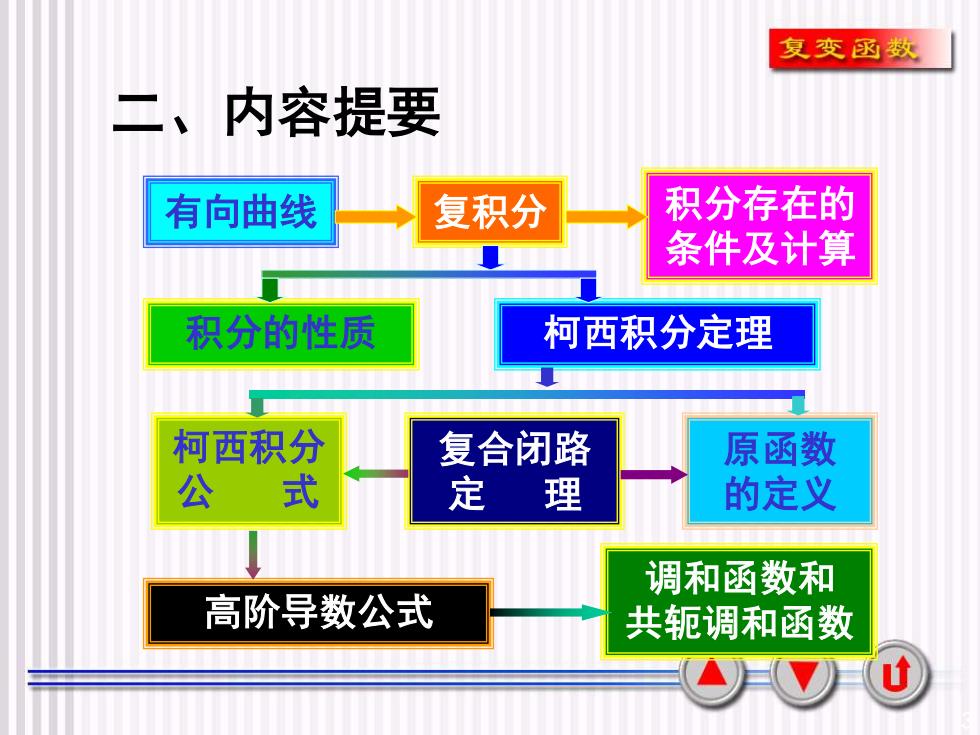
复变函数二、内容提要积分存在的复积分有向曲线条件及计算积分的性质柯西积分定理柯西积分原函数复合闭路公式的定义定理调和函数和高阶导数公式共轭调和函数U
3 二、内容提要 有向曲线 复积分 积分存在的 条件及计算 积分的性质 柯西积分定理 原函数 的定义 复合闭路 定 理 柯西积分 公 式 高阶导数公式 调和函数和 共轭调和函数
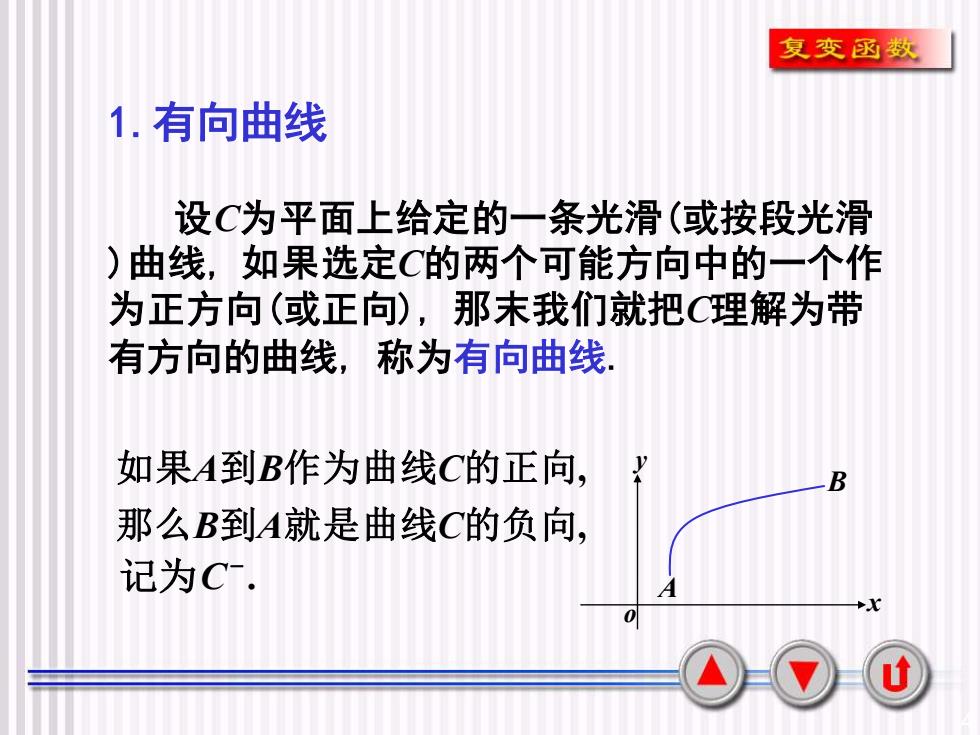
复变函数1.有向曲线设C为平面上给定的一条光滑(或按段光滑)曲线,如果选定C的两个可能方向中的一个作为正方向(或正向),那未我们就把C理解为带有方向的曲线,称为有向曲线如果A到B作为曲线C的正向B那么B到A就是曲线C的负向,记为C-.+xOu
4 设C为平面上给定的一条光滑(或按段光滑 )曲线, 如果选定C的两个可能方向中的一个作 为正方向(或正向), 那末我们就把C理解为带 有方向的曲线, 称为有向曲线. x y o A 如果A到B作为曲线C的正向 B , 那么B到A就是曲线C的负向, . − 记为C 1.有向曲线
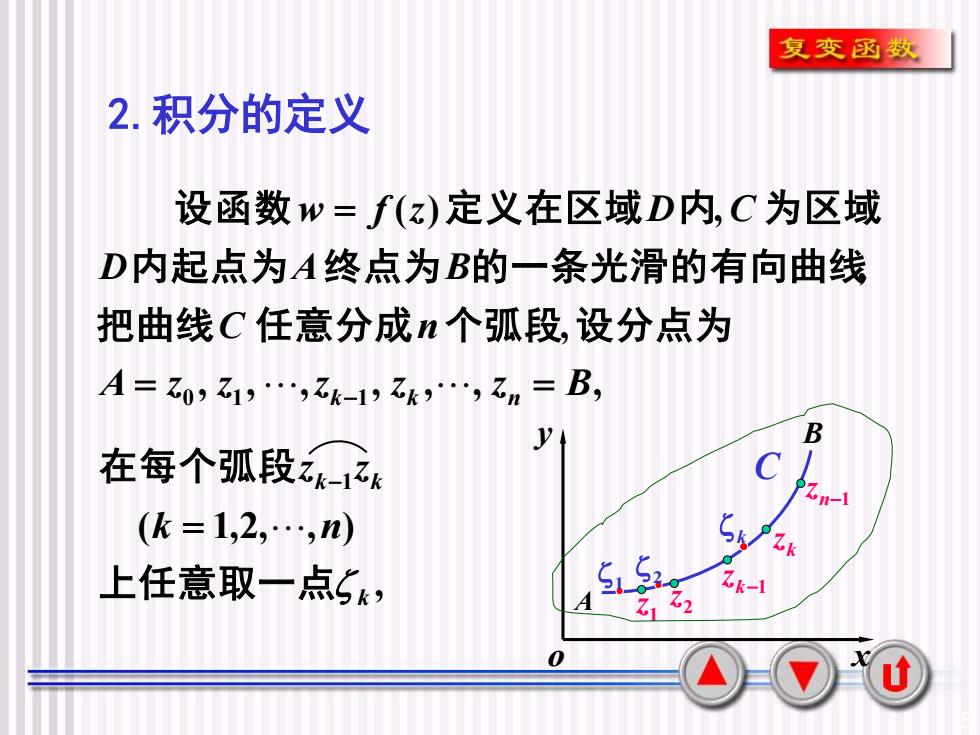
复变函数2.积分的定义设函数w = f(z)定义在区域D内,C为区域D内起点为A终点为B的一条光滑的有向曲线把曲线C任意分成n个弧段,设分点为A= Zo, Z1, -, k-1, Zk,-, Zn = B,ByC1在每个弧段zk-1zkZ.n-1CH(k = 1,2,.,n)T52s.Zk-1上任意取一点5k22AZ0u
5 2.积分的定义 , , , , , , , , , ( ) , A z0 z1 z 1 z z B C n D A B w f z D C = k k n = = − 把曲线 任意分成 个弧段 设分点为 内起点为 终点为 的一条光滑的有向曲线 设函数 定义在区域 内 为区域 o x y A B n−1 z k z k−1 z 2 z 1 z k C 1 2 , ( 1,2, , ) 1 k k k k n z z 上任意取一点 在每个弧段 = −